1. 概述
已知相机参数和匹配点,恢复三维点的坐标。如下图所示:
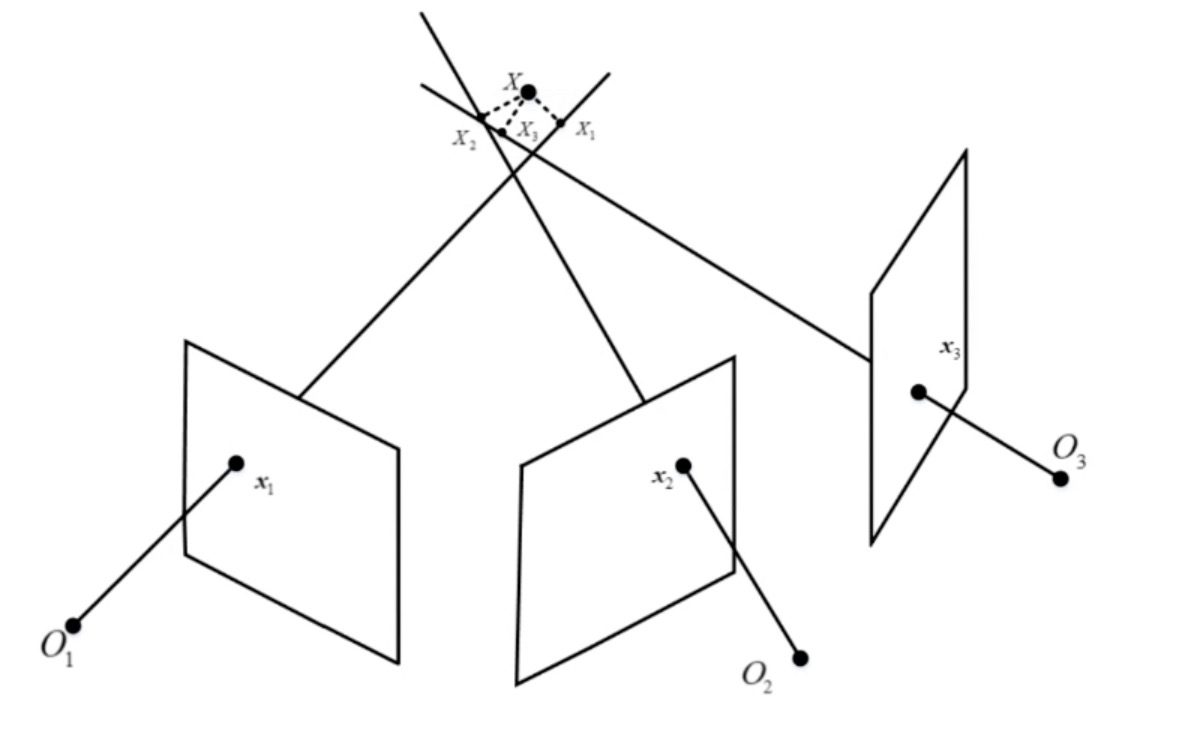
第i个相机投影矩阵如下所示:
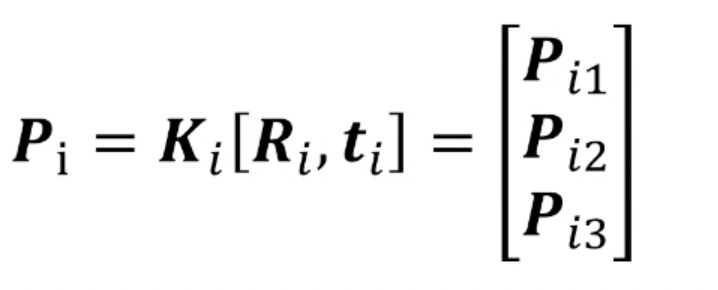
给定检测和匹配的三个特征点,$x_1$, $x_2$和$x_3$,空间三维点坐标为$\bf{X} = [x, y, z, 1]^T$,对应在第i个视角中投影的图像坐标为$\bf{x}_i = [x_i, y_i, 1]^T$。那么理想情况下,这三条射线相较于同一个点。但是,由于误差的存在,这三个点的射线并不能够准确相较于一点。此时,可采用最小二乘来求解。
2. 算法详解
根据投影方程$\bf{d}_{i}\bf{x}_{i} = \bf{P}_{i}\bf{X}$,等式两侧同时叉乘$\bf{x}_i$,得到:
$\bf{x}_i \times (\bf{P}_{i}\bf{X}) = \bf{0}$,
其中,$\bf{x}_i = [x_i, y_i, 1]^T$,那么,我们得到:
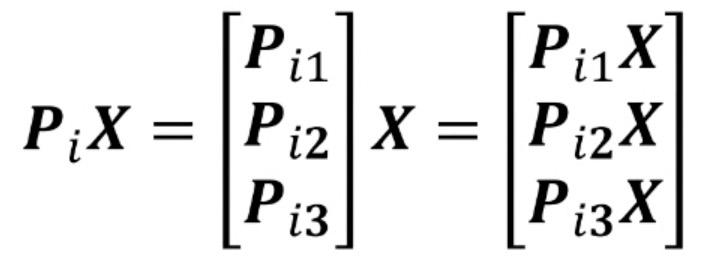
该矩阵为3行1列的。根据向量叉乘的运算,展开的:
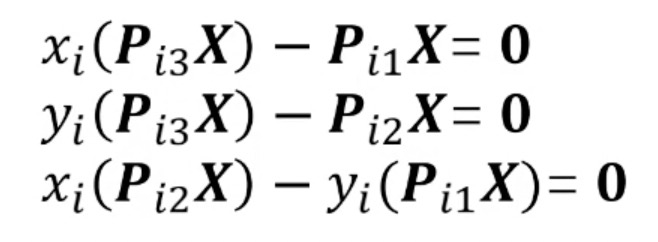
由于最后一行可以通过前两行计算得到,因此,化简得到:
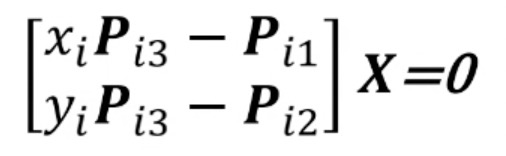
1个观测点可以提供2个约束,$\bf{X}$有3个自由度,求解该方程至少需要2对匹配点,即$\bf{A}\bf{X} = \bf{0}$,其中$\bf{A}$为:
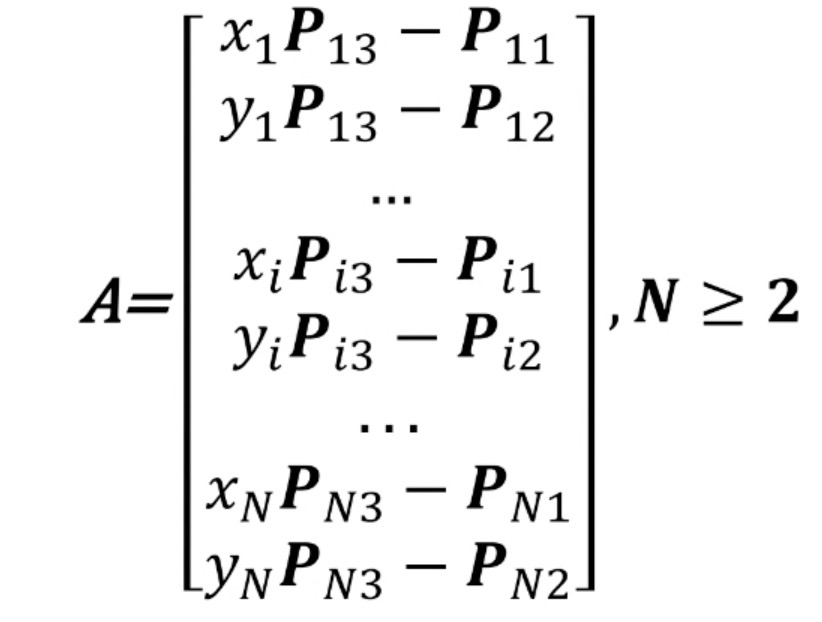
此时可对$\bf{A}$进行SVD分解,求得$\bf{X}$。
宽基线求解更加稳定,在匹配成功的点中,选择宽基线中的匹配对进行三角化求解。对track进行排序,来找到宽基线的匹配点。如果存在外点,采用RANSAC算法来进行精确求解。流程如下所示:
- 计算RANSAC采样次数,设置内点阈值(重投影误差);
- 随机采样一对视角,计算三维点坐标;
- 计算每个视角中的重投影误差,统计内点个数;
- 重复上述步骤,直到满足采样次数,选择内点最多的视角;
- 利用所有内点重新计算三维点坐标。
3. 代码实现
1 |
|
4. 总结和讨论
- 三角量测的矛盾点
- 在同样的相机分辨率下,平移越大,三角化测量就会越精确;但是平移越大,将会导致图像的外观发生明确变化,这会使得特征的提取和匹配变得更困难