1. 概述

PnP为Perspective-n-Point的简称，是求解3D到2D点对的运动的方法，即给出n个3D空间点时，求解相机的内外参数问题。比如，我们在一幅图像中，知道其中至少四个图像中确定的点在3D空间下的相对坐标位置，我们就可以估计出相机相对于这些点的姿态，或者说估计出这些3D点在相机坐标系下姿态。如下图所示：

（图片来源：基于图像的三维重建）

典型的PnP问题求解方式有很多种，例如P3P，直接线性变换(DLT), EPnP(Efficient PnP), UPnP和Bundle Adjustment。

2. 算法详解

2.1 DLT算法

直接线性变换法的主要思想是构造线性方程组来求解参数。一直三维点坐标X, Y和Z，像素坐标u和v，求解内参K、旋转矩阵R和平移向量t。我们首先得到如下等式：

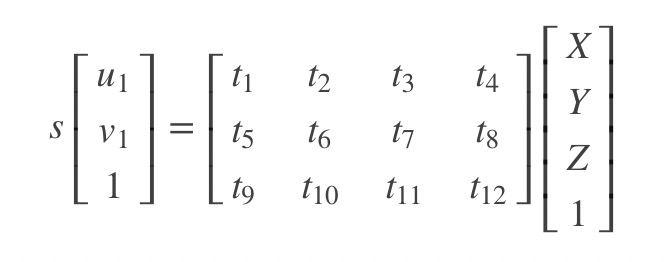
消去s后可得到约束：

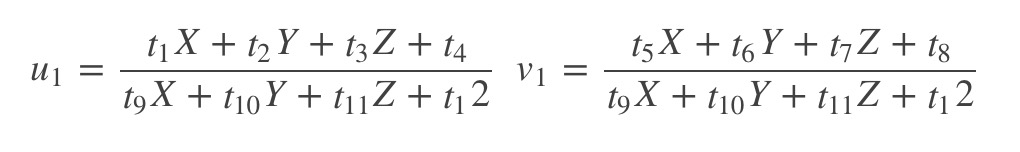
假设：

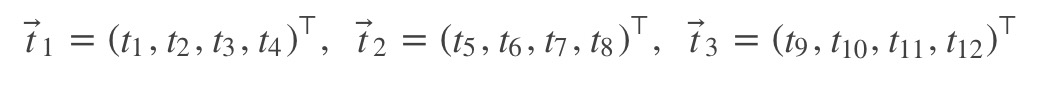
那么得到：

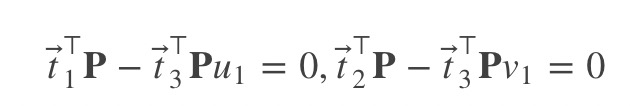
当存在N个匹配点对时，我们得到：

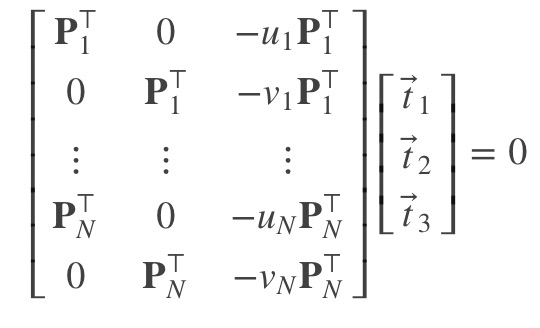
一共12个未知数，每对3D和2D匹配点提供2个线性约束，因此共需要至少6对对应点，才可以求得$\bf{t}_1$, $\bf{t}_2$和$\bf{t}_3$，即求得矩阵$\bf{T} = [\bf{K}\bf{R}, \bf{K}\bf{t}]$。

（1）求解内参和旋转

已知$T(:, 1:3) = \bf{K}\bf{R}$，且内参矩阵$\bf{K}$为上三角矩阵，$\bf{R}$为正交矩阵。对矩阵$T(:, 1:3)^{-1}$进行QR分解，分别得到$\bf{R}^{-1}$以及$\bf{K}^{-1}$，进而得到内参矩阵$\bf{K}$以及旋转矩阵$\bf{R}$。

（2）求解平移

已知$T(:, 4) = \bf{K}\bf{t}$，以及内参矩阵$\bf{K}$，可得平移向量$\bf{t}$。

DLT算法要求$\bf{R}$正交，导致其求解不稳定。

2.2 P3P算法

我们首先需要知道的是P3P并不是直接根据3D-2D点求出相机位姿矩阵，而是先求出对应的2D点在当前相机坐标系下的3D坐标，然后根据世界坐标系下的3D坐标和当前相机坐标系下的3D坐标求解相机位姿的。P3P的求解是从余弦定理开始的，设相机坐标中心为点O，A、B、C为不共线的三个3D点，D为验证3D点，如下图所示：

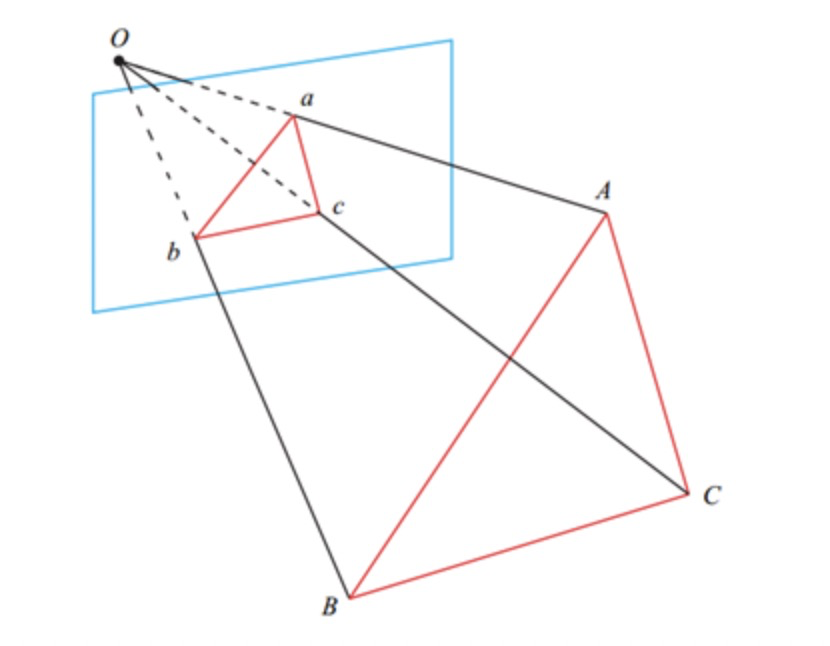
其中A, B和C为世界坐标系。图中为3D到3D的对应点，所以是把PnP问题转化为ICP问题。先利用三角形近似关系有以下三角形相似：

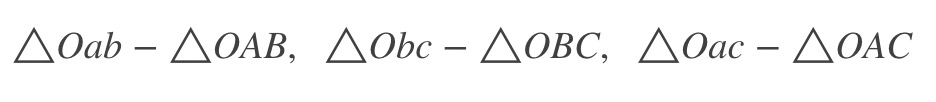
考虑余弦关系：

左右两边同时除以$OC^2$, 令$x = \frac{OA}{OC}$, $y = \frac{OB}{OC}$有：

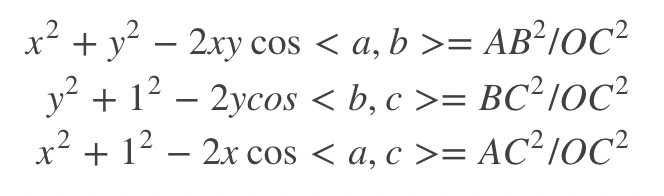
再令$u = \frac{AB^2}{OC^2}$, $v = \frac{BC^2}{AB^2}$, $w = \frac{AC^2}{AB^2}有:

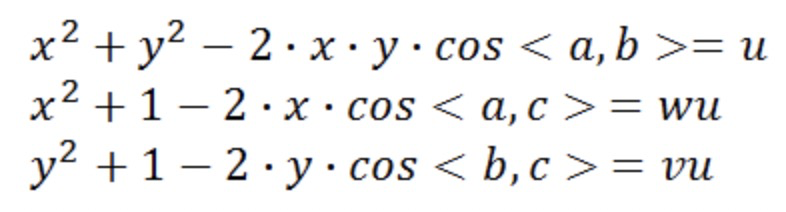
从上式中先解出v，代入第二和第三个式子，有:

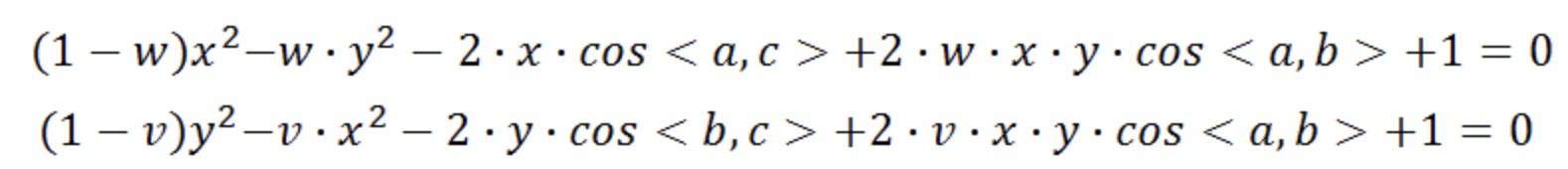
接下来的过程就是如何通过上述两个式子求解A，B，C在当前相机坐标系下的坐标。首先需要明确的是哪些量是已知量，输入的是3D和2D的坐标，即：

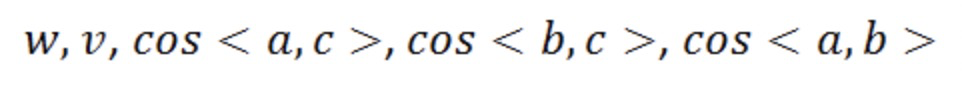
因为首先AB，BC，AC的距离都是可以根据输入的3D点求得，而输入的2D点可以求解三个余弦值（如何求解，像素坐标根据相机内参矩阵和畸变参数可以求得在归一化图像平面上的3D坐标，此时$z = 1$，故余弦值可求）。此时未知数仅x，y两个，所以理论上两个未知数两个方程，是可求的。（从x，y求PA，PB，PC也可求）。

3. 代码实现

#include <iostream>
#include <opencv2/opencv.hpp>

void find_rt(cv::Mat iamge ,cv::Mat matrix ,cv::Mat dist_coeffs ,cv::Mat& rvec_mat,cv::Mat& tvec_mat ) {
    zz::CalibrationMonocular cm;
    std::vector<cv::Point2f> image_points;
    cm.find_circle(iamge,image_points,cv::Size(4,11),1);

    std::vector<cv::Point3f> image_points_in3d;
    cm.init_cicle_opencv_3dpoints(cv::Size(4,11),image_points_in3d,1,1);
    cv::solvePnP(image_points_in3d,image_points,matrix,dist_coeffs,rvec_mat,tvec_mat);
}

int main(int argc, char *argv[]) {
    cv::Mat image;
    image = cv::imread(argv[1]);
    cv::Mat intrinsic = cv::Mat(3, 3, CV_64FC1, cv::Scalar::all(0));
    cv::Mat distortion = cv::Mat(1, 5, CV_64FC1, cv::Scalar::all(0));
    intrinsic.at<double>(0, 0) = 2469.453065156600600;
    intrinsic.at<double>(1, 1) = 2470.233140630011300;
    intrinsic.at<double>(0, 2) = 1991.786856389101300;
    intrinsic.at<double>(1, 2) = 1500.165893152338400;
    intrinsic.at<double>(2, 2) = 1;

    distortion.at<double>(0, 0) = 0.031219512203754;
    distortion.at<double>(0, 1) = -0.063477515747468;
    distortion.at<double>(0, 2) = 0.000016372054794;
    distortion.at<double>(0, 3) = -0.000635253902664;
    distortion.at<double>(0, 4) = 0.000000000000000;
    
    cv::Mat l_rvec_mat, l_tvec_mat;
    cv::Mat cover_left_image;
    cover_left_image = image.clone();
    cv::rectangle(cover_left_image, cv::Point(0,0), cv::Point(2000,3000), cv::Scalar(0, 0, 255), -1, 8, 0);
    find_rt(cover_left_image, intrinsic, distortion, l_rvec_mat, l_tvec_mat);
    
    return 0;
}

4. 总结和讨论

P3P的问题：

只利用三个点的信息，当给定的配对点多于3组时，难以利用更多的信息
如果数据点存在噪声时，或者匹配是误匹配的情况下，算法失败

5. 参考

PNP(pespective-n-point)算法学习笔记