路径规划（九）-RRT-Star算法

发表于 | 分类于 ，

1. 概述

回顾RRT算法，虽然能快速地找到路径，但是得到的路径并不光滑，对机器人移动而言不是最优路径。因此，本文我们介绍优化RRT的算法，即RRT*算法。RRT*与RRT算法流程基本相同，不同之处就在于最后加入将$X_{new}$加入搜索树时父节点的选择策略上不同。

2. 算法详解

RRT算法选择新节点$X_{new}$时，基于随机点和最近邻点，前进制定步长生成。而在RRT*算法中，在选择父节点时会有一个重连(Rewire)过程，也就是以$X_{new}$为圆心，半径为r的邻域内，找到与$X_{new}$连接后，代价(从起点移动到$X_{new}$的路程)最小的节点，并选择该节点作为$X_{new}$的父节点，而不是$X_{near}$。RRT*算法详见下图：

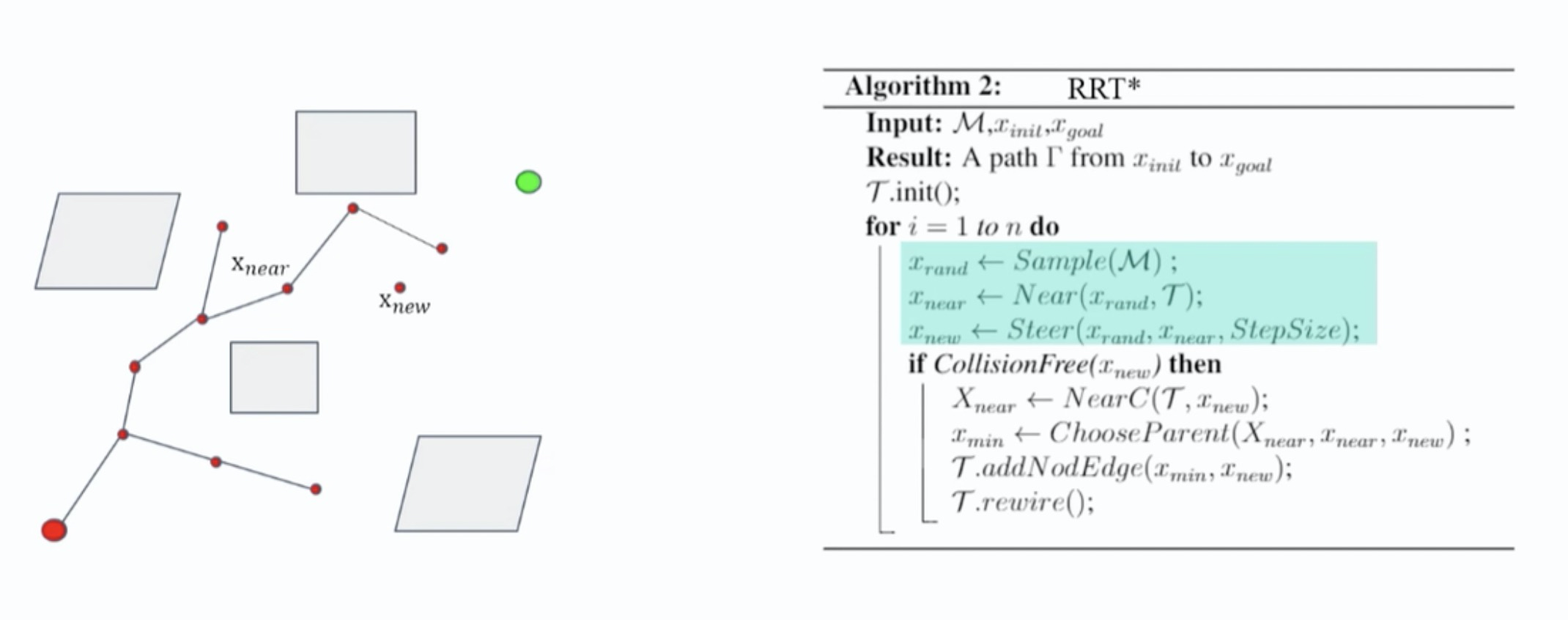
image-20210410123739640

算法步骤：

  • 随机采样、寻找最近和确定新节点

  • 以一定半径，重新选择父节点，选择标准是从初始节点到新节点路径cost最小的路径上的节点作为新节点的父节点，如下图所示：

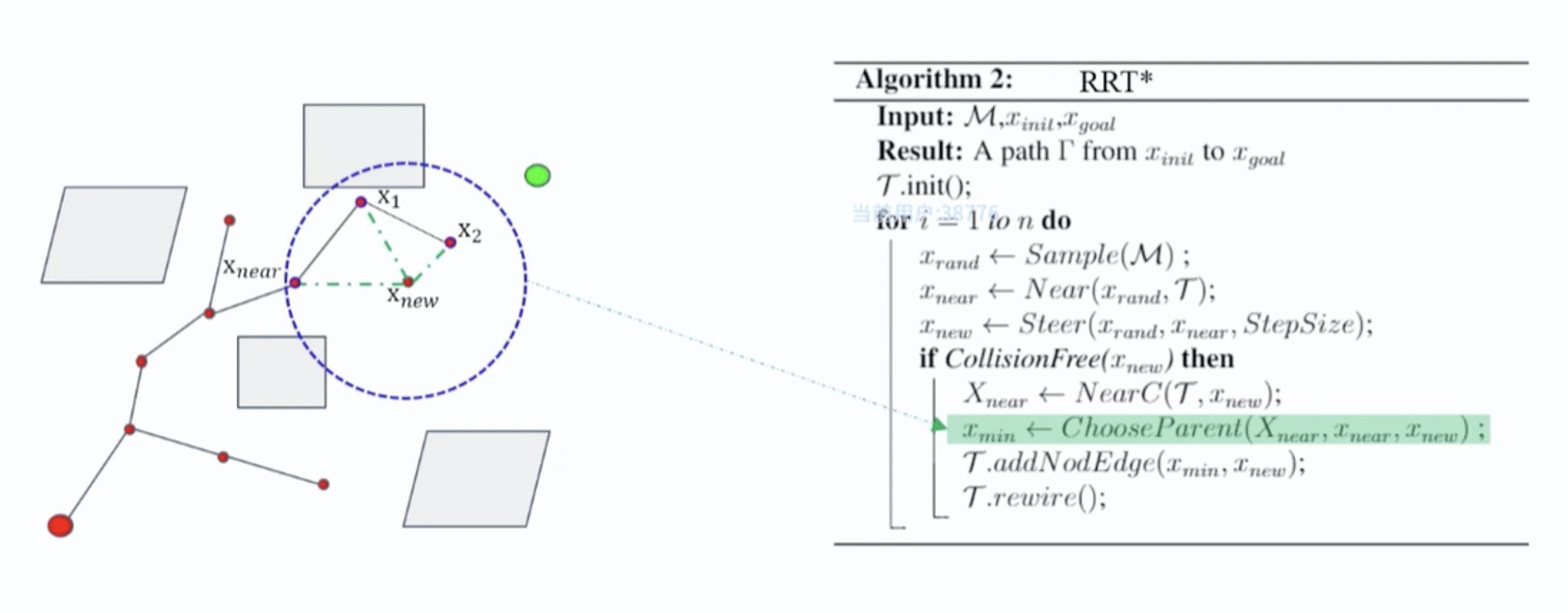
    image-20210410124336404

  • 重布线，对树中的节点，根据起始点到当前节点的cost进行重布线，修改节点的父节点，如下图所示，$x_2$的父节点更改为$x_{new}$：

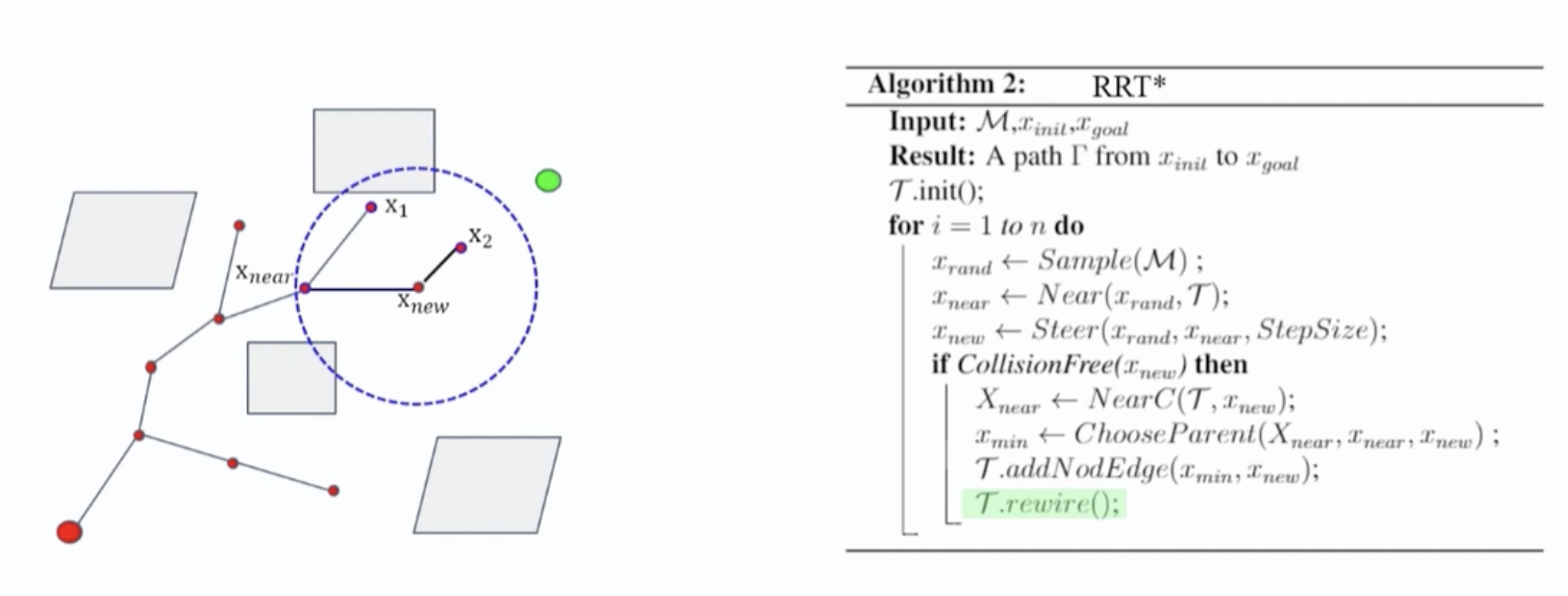
    image-20210410134036814

重布线过程的意义在于每当生成了新的节点后，是否可以通过重新布线，使得某些节点的路径代价减少。如果以整体的眼光看，并不是每一个重新布线的节点都会出现在最终生成的路径中，但在生成随机树的过程中，每一次的重布线都尽可能的为最终路径代价减小创造机会。加入重连步骤后，可以确保在$X_{new}$的邻域范围得到的路径是最优的，所以相较于RRT算法得到的路径，RRT*算法得到的路径更为平直。

3. 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
import numpy as np
import time
import random
import matplotlib
import matplotlib.pyplot as plt
import math
import copy


def get_map(image):
    ima = matplotlib.image.imread(image)
    return ima


def random_point():
    r_x = random.random() * (m_map.shape[0] - 1)
    r_y = random.random() * (m_map.shape[1] - 1)
    return [r_x, r_y]


def feasible_point(p):
    if 0 <= p[0] < m_map.shape[0] and 0 <= p[1] < m_map.shape[1] and m_map[int(p[0])][int(p[1])][0] == 255:
        return True
    else:
        return False


def distance(p, q):
    d = abs(p[0] - q[0]) + abs(p[1] - q[1])
    return d


def nearest(p, tree):
    row, min_d = -1, float('INF')
    for i in range(len(tree)):
        p_n = [tree[i][0], tree[i][1]]
        td = distance(p_n, p)
        if td < min_d:
            min_d = td
            row = i
    p_near = [tree[row][0], tree[row][1]]
    return p_near, row


def extend(p, q, step):
    if distance(p, q) < thresh_hold:
        return q
    else:
        theta = math.atan2((q[1] - p[1]), (q[0] - p[0]))
        p_new = [p[0] + step * math.cos(theta), p[1] + step * math.sin(theta)]
        return p_new


def cost(i, tree):
    c = 0
    while True:
        t = tree[i][2]
        if t == -1:
            break

        c += distance(tree[i][:2], tree[t][:2])
        i = t
    return c


def get_nearby(r, p, tree):
    p_nearby = []
    for i in range(len(tree)):
        p_n = [tree[i][0], tree[i][1]]
        if feasible_point(p_n):
            td = distance(p_n, p)
            if td < r:
                p_nearby.append([p_n, i])
    return p_nearby


def new_father(p_new, p_nearby, tree):
    min_dis, t = float('inf'), -1
    min_father = []
    for i in range(len(p_nearby)):
        t_dis = distance(p_new, p_nearby[i][0]) + cost(p_nearby[i][1], tree)
        if t_dis < min_dis and checkpath(p_nearby[i][0], p_new, 1):
            min_dis = t_dis
            min_father = p_nearby[i]
            t = i
    p_nearby.pop(t)
    if min_father:
        tree.append([p_new[0], p_new[1], min_father[1]])

    i_p_new = len(tree)-1
    cost_p_new = cost(i_p_new, tree)
    for j in p_nearby:
        pre_cost = cost(j[1], tree)
        if cost_p_new + distance(j[0], p_new) < pre_cost and checkpath(p_new, j[0], 1):
            tree[j[1]][2] = i_p_new


def checkpath(p, q, step):
    if distance(p, q) < thresh_hold:
        return True

    theta = math.atan2((q[1] - p[1]), (q[0] - p[0]))
    t = copy.deepcopy(p)
    while distance(t, q) > thresh_hold:
        t = [t[0] + step * math.cos(theta), t[1] + step * math.sin(theta)]
        if not feasible_point(t):
            return False
    return True


def pruning(path, step):
    new_path = [path[0]]
    i = 0
    j = 1
    while i < len(path)-2 and j < len(path):
        if checkpath(path[i], path[j], step):
            if distance(path[j], path[-1]) < thresh_hold:
                new_path.append(path[-1])
                break
            j += 1
        else:
            new_path.append(path[j-1])
            i = j-1
    new_cost = 0
    for i in range(len(new_path)-1):
        new_cost += distance(new_path[i], new_path[i+1])
    return new_path, new_cost


def interp(path, step):
    i_path = [path[0]]
    i = 0
    t = copy.deepcopy(path[0])
    while i < len(path)-1:
        theta = math.atan2((path[i+1][1] - path[i][1]), (path[i+1][0] - path[i][0]))
        while distance(t, path[i+1]) > thresh_hold:
            t = [t[0] + step * math.cos(theta), t[1] + step * math.sin(theta)]
            i_path.append(t)
        t = copy.deepcopy(path[i+1])
        i += 1
    return i_path


def rrt(step, thresh_hold, init, goal, radius, iterations):
    max_attempts, label, i_goal = iterations, 0, -1
    tree = list()
    tree.append(init + [-1])

    count = 0
    while count < max_attempts:
        p_rand = random_point()
        p_near, row = nearest(p_rand, tree)
        p_new = extend(p_near, p_rand, step)

        if not feasible_point(p_new):
            count += 1
            continue

        if distance(p_new, goal) <= thresh_hold:
            tree.append([goal[0], goal[1], row])
            i_goal = len(tree) - 1
            label = 1
            continue

        p_new_near, n_row = nearest(p_new, tree)
        if distance(p_new, p_new_near) < thresh_hold:
            count += 1
            continue

        p_nearby = get_nearby(radius, p_new, tree)
        new_father(p_new, p_nearby, tree)

    if label == 1:
        print("found path")
        path = []
        i = i_goal
        next_i = tree[i][2]
        while next_i != -1:
            path.append([tree[i][0], tree[i][1]])
            i = next_i
            next_i = tree[i][2]
        path.append([init[0], init[1]])
        c = cost(i_goal, tree)
        return path[::-1], tree, c
    else:
        print('reached max attempts')
        return tree


if __name__ == '__main__':
    m_map = get_map('map_2.bmp')

    m_map = m_map.swapaxes(0, 1)
    init = [10, 10]
    goal = [490, 490]
    step = 15
    thresh_hold = 15
    radius = 30
    iterations = 5000

    path, tree, cost = rrt(step, thresh_hold, init, goal, radius, iterations)

    print('cost: ', cost)
    x = [i[0] for i in path]
    y = [i[1] for i in path]
    p_tree, tx, ty = [], [], []
    for i in tree:
        tx.append(i[0])
        ty.append(i[1])

    plt.plot(x, y, color="darkblue")
    plt.scatter(tx, ty, color='lightsteelblue', s=5)

    new_path, new_cost = pruning(path, step)
    print('new_cost: ', new_cost)
    n_x = [i[0] for i in new_path]
    n_y = [i[1] for i in new_path]
    plt.plot(n_x, n_y, color="green")

    i_path = interp(new_path, step)
    i_x = [i[0] for i in i_path]
    i_y = [i[1] for i in i_path]

    m_map = m_map.swapaxes(0, 1)
    plt.imshow(m_map)

    plt.show()

参考：https://github.com/hichenway/sampling-based-path-planning

4. 总结和讨论

RRT*算法迭代的时间越久，就越可以得到相对满意的规划路径。

5. 参考