1. 概述

空间索引在多维数据处理中已被广泛应用，常见空间索引一般是自顶向下逐级划分空间的各种空间索引结构，比较有代表性的包括 BSP树、 KD树、 KDB树、 R树、 R+树、 CELL树、四叉树和八叉树等索引结构，而在这些结构中KD树和八叉树在3D点云数据组织中应用较为广泛。KD-Tree简称k维树，是一种空间划分的数据结构，本质上是一种二叉树，常被用于高维空间中的搜索，比如范围搜索和最近邻搜索。KD-Tree用来组织表示K维空间中点集合，是一种带有其他约束条件的二分查找树。如果特征的维度是D，样本的数量是N，那么一般来讲kd树算法的复杂度是O(DlogN)，相比于穷算的O(DN)省去了非常多的计算量。

KD-Tree求解的问题如下所示：

给定一堆已有的样本数据，和一个被询问的数据点，如何找到离五角星最近的n个点？

基本解法
- 遍历，按照一定距离选取最近的n个点
- 计算复杂度为O(DN)
高级解法
- KD-Tree，时间复杂度为O(DlogN)
- …

2. 算法详解

KD-Tree数据结构主要分为两个步骤：KD-Tree的构建和查询。

2.1 构建阶段

构建就是按照某种顺序将无序化的点云进行有序化排列，方便进行快捷高效的检索。

一些术语定义如下：

分裂点（split_point）
分裂方式（split_method）
左儿子（left_son）
右儿子（right_son）

数据结构如下所示：

struct kdtree{
    Node-data - 数据矢量   数据集中某个数据点，是n维矢量（这里也就是k维）
    Range     - 空间矢量   该节点所代表的空间范围
    split     - 整数       垂直于分割超平面的方向轴序号
    Left      - kd树       由位于该节点分割超平面左子空间内所有数据点所构成的k-d树
    Right     - kd树       由位于该节点分割超平面右子空间内所有数据点所构成的k-d树
    parent    - kd树       父节点  
}

建树规则如下：

针对空间的“维”的
节点的状态中的：分裂方式（split_method）
建树依据
- 主要思想：先计算当前区间[L, R]中（这里的区间是点的序号区间，而不是我们实际上的坐标区间），每个点的坐标的每一维度上的方差，取方差最大的那一维，设为d，作为分裂方式（split_method ），把区间中的点按照在d上的大小，从小到大排序，取中间的点sorted_mid作为当前节点记录的分裂点，然后，再以[L, sorted_mid-1]为左子树建树，以[sorted_mid+1, R]为右子树建树，迭代进行上述步骤
- 初始化分割轴
  - 取方差最大的轴为初始分割轴，例如X轴
- 确定当前节点
  - 选取中位数为当前点
- 划分双支数据
  - 在X轴维度上，比较和中位数的大小，进行划分左支和右支
- 更新分割轴
  - 下一个维度为X轴
- 迭代进行上述步骤，直到全部分支构建完毕

示例参考：https://www.joinquant.com/view/community/detail/c2c41c79657cebf8cd871b44ce4f5d97和https://blog.csdn.net/FAICULTY/article/details/79474627

给定如下数据
- (2, 3), (5, 4), (9, 6), (4, 7), (8, 1), (7, 2)
数据维度只有2维，所以可以简单地给x，y两个方向轴编号为0,1，即split={0,1}
以X轴为切分轴，基于X轴对数据进行排序，选取中间数据(7, 2)作为根节点
- 对于左侧数据，以Y轴为切分轴，对数据进行排序，选取中间数据(5, 4)作为左树的子节点
- 再对于左侧数据，迭代进行上一步，直到所有左侧数据均被划分完成
对于右侧数据，以X轴为切分轴，选取中间数据(9, 6)作为根节点的左支
- 对于右侧数据，迭代进行上一步，直到所有数据均被划分完成

上述数据的KD-Tree划分结果如下图所示：

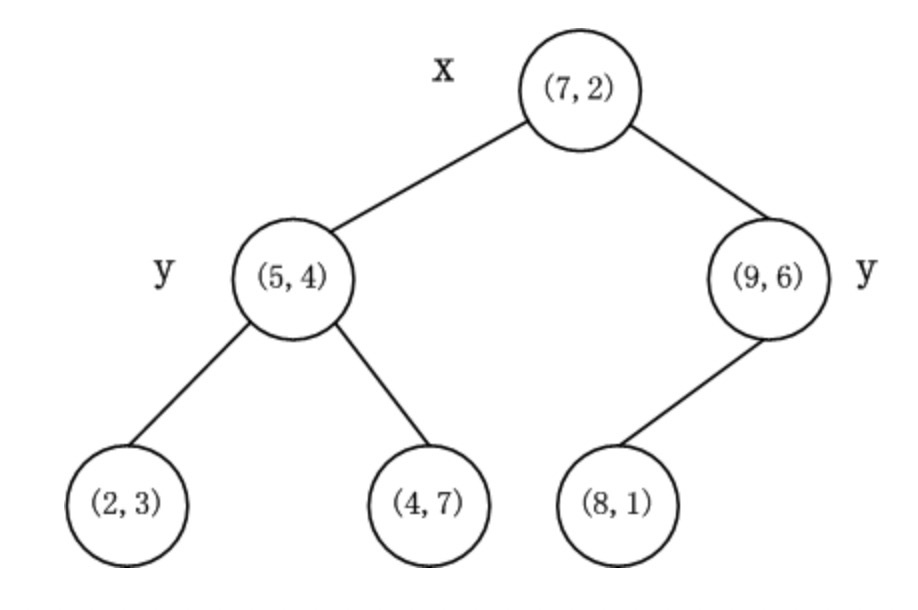
即：

{
    'split': 0,
    'median': array([
        7.,
        2.
    ]),
    'left': {
        'split': 1,
        'median': array([
            5.,
            4.
        ]),
        'left': {
            'split': 0,
            'median': array([
                2.,
                3.
            ]),
            'left': None,
            'right': None
        },
        'right': {
            'split': 0,
            'median': array([
                4.,
                7.
            ]),
            'left': None,
            'right': None
        }
    },
    'right': {
        'split': 1,
        'median': array([
            9.,
            6.
        ]),
        'left': {
            'split': 0,
            'median': array([
                8.,
                1.
            ]),
            'left': None,
            'right': None
        },
        'right': None
    }
}

2.2 查询

给定一个构建于一个样本集的kd树，下面的算法可以寻找距离某个点p最近的k个样本。

查询的示例参考：https://www.joinquant.com/view/community/detail/c2c41c79657cebf8cd871b44ce4f5d97

步骤：

第一步：假设搜索的节点为p，一个有k个空位的列表，用于保存已搜寻到的最近点
第二步：根据p的坐标值和每个节点的切分进行向下搜索，例如按照切分方向（向X轴或者Y轴）进行搜索，如果p的坐标小于切分节点坐标，则向左搜索，反之，向右搜索
第三步：当达到一个底部节点时，将其标记为访问过
- 如果L里不足k个点，则将当前节点的特征坐标加入L
- 如果L不为空并且当前节点的特征与p的距离小于L里最长的距离，则用当前特征替换掉L中离p最远的点
第四步：如果当前节点不是整棵树最顶端节点下述步骤；反之，输出L，算法完成
- 向上爬一个节点
  - 如果当前（向上爬之后的）节点未曾被访问过，将其标记为被访问过，然后执行下述步骤
    - 如果此时L里不足k个点，则将节点特征加入L
    - 如果L中已满k个点，且当前节点与p的距离小于L里最长的距离，则用节点特征替换掉L中离最远的点
  - 计算p和当前节点切分线的距离
    - 如果该距离大于等于L中距离p最远的距离并且L中已有k个点，则在切分线另一边不会有更近的点，执行第四步
    - 如果该距离小于L中最远的距离或者L中不足k个点，则切分线另一边可能有更近的点，因此在当前节点的另一个枝从第二步开始执行

实际例子，参考：https://www.joinquant.com/view/community/detail/c2c41c79657cebf8cd871b44ce4f5d97。

3. 代码实现

import numpy as np
import matplotlib.pyplot as plt


def load_data(fileName):
    dataMat = []
    with open(fileName) as fd:
        for line in fd.readlines():
            data = line.strip().split()
            data = [float(item) for item in data]
            dataMat.append(data)
    dataMat = np.array(dataMat)
    label = dataMat[:, 2]
    dataMat = dataMat[:, :2]
    return dataMat, label


def create_KDTree(dataSet, depth):
    n = np.shape(dataSet)[0]
    treeNode = {}
    if n == 0:
        return None
    else:
        n, m = np.shape(dataSet)
        split_axis = depth % m
        depth += 1
        treeNode['split'] = split_axis
        dataSet = sorted(dataSet, key=lambda a: a[split_axis])
        num = n // 2
        treeNode['median'] = dataSet[num]
        treeNode['left'] = create_KDTree(dataSet[:num], depth)
        treeNode['right'] = create_KDTree(dataSet[num + 1:], depth)
        return treeNode


def search_KDTree(tree, data):
    k = len(data)
    if tree is None:
        return [0] * k, float('inf')

    split_axis = tree['split']
    median_point = tree['median']
    if data[split_axis] <= median_point[split_axis]:
        point_nearest, distance_nearest = search_KDTree(tree['left'], data)
    else:
        point_nearest, distance_nearest = search_KDTree(tree['right'], data)

    distance = np.linalg.norm(data - median_point)
    if distance < distance_nearest:
        distance_nearest = distance
        point_nearest = median_point.copy()

    distance_split = abs(data[split_axis] - median_point[split_axis])
    if distance_split > distance_nearest:
        return point_nearest, distance_nearest
    else:
        if data[split_axis] <= median_point[split_axis]:
            subtree = tree['right']
        else:
            subtree = tree['left']

        point_near, distance_neardistance = search_KDTree(subtree, data)
        if distance_neardistance < distance_nearest:
            distance_nearest = distance_neardistance
            point_nearest = point_near.copy()

        return point_nearest, distance_nearest


if __name__ == '__main__':
    dataMat, label = load_data('test.txt')
    fig = plt.figure(0)
    ax = fig.add_subplot(111)
    ax.scatter(dataMat[:, 0], dataMat[:, 1], c=label, cmap=plt.cm.Paired)

    tree = create_KDTree(dataMat, 0)
    print(tree)

    point = [2, 4.5]
    nearpoint, neardis, = search_KDTree(tree, point)
    ax.scatter(point[0], point[1], c='g', s=50)
    ax.scatter(nearpoint[0], nearpoint[1], c='r', s=50)

    plt.show()

参考：https://github.com/guoswang/K-D-Tree和https://github.com/stefankoegl/kdtree

4. 总结和讨论

Kd树在维度较小时（比如20、30），算法的查找效率很高，然而当数据维度增大（例如：K≥100），查找效率会随着维度的增加而迅速下降。假设数据集的维数为D，一般来说要求数据的规模N满足N>>2的D次方，才能达到高效的搜索。

空间数据结构（一）-KD-Tree