路径规划（八）-RRT算法

1. 概述

RRT是Steven M. LaValle和James J. Kuffner Jr.提出的一种通过随机构建Space Filling Tree实现对非凸高维空间快速搜索的算法。该算法可以很容易的处理包含障碍物和差分运动约束的场景，因而广泛的被应用在各种机器人的运动规划场景中。RRT算法及其变种包括Basic RRT、基于概率的RRT、RRT Connect和RRT*算法。本文主要介绍basic RRT、基于概率的RRT和RRT Connect算法，后续再介绍RRT*算法。

2. 算法详解

2.1 Basic RRT算法

原始的RRT算法，即basic RRT算法，将搜索的起点位置作为根节点，然后通过随机采样增加叶子节点的方式，生成一个随机扩展树，当随机树的叶子节点进入目标区域，就得到了从起点位置到目标位置的路径。相比较于PRM算法，RRT算法不需要区分学习和搜索阶段。算法伪代码如下图所示，其中M是地图环境，$X_{init}$是起始节点，$X_{goal}$是目标节点：

算法主要思想：

• 将起点初始化为搜索树T的根节点$X_{init}$
• 在空间中采样点$X_{rand}$，按照设定的随机采样概率进行随机采样，其余情况直接将目标点作为采样点
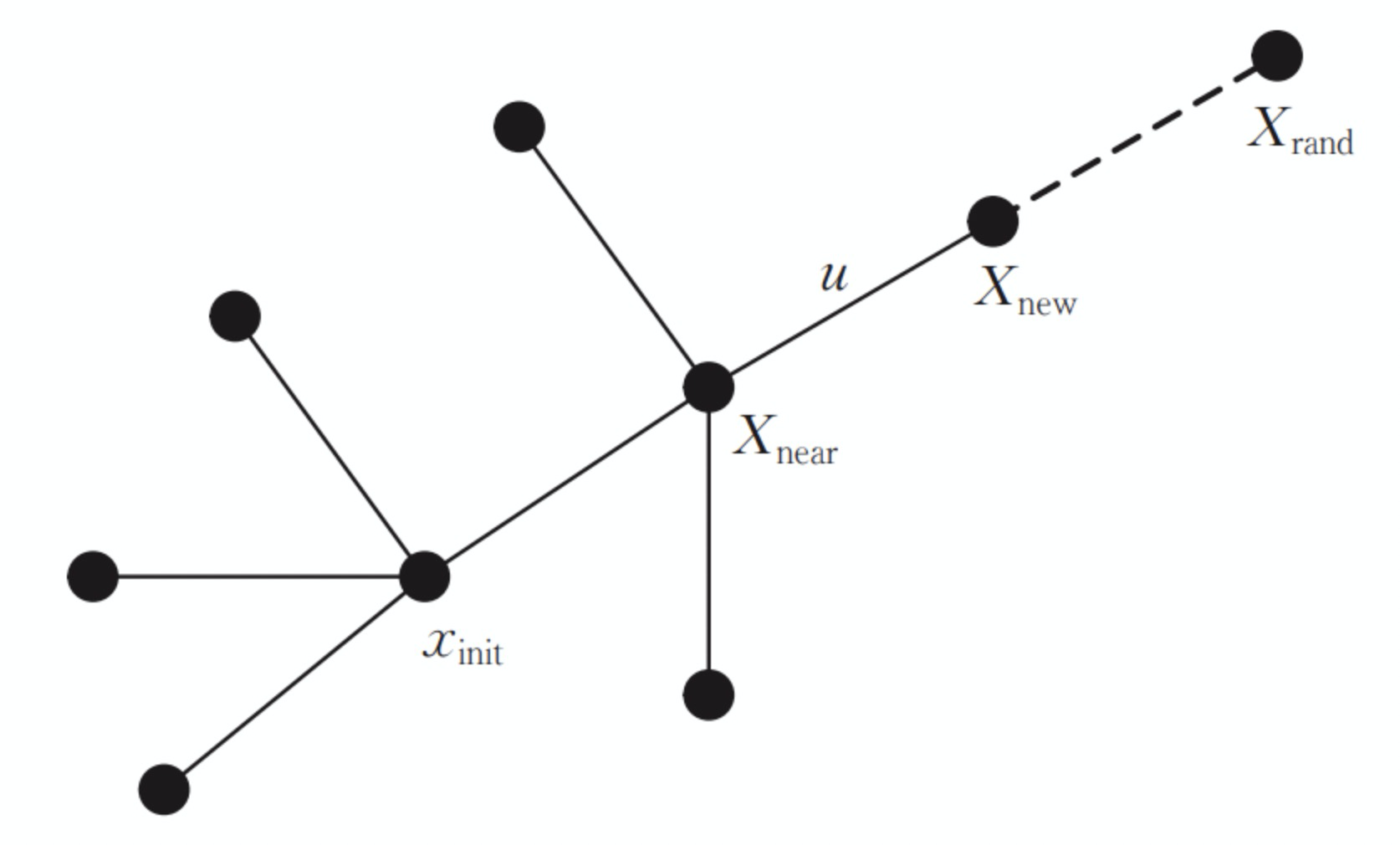
• 从搜索树T中取出距离采样点$X_{rand}$最近的节点$X_{near}$
• 沿着$X_{near}$到$X_{rand}$方向前进Step size，得到$X_{new}$，继而得到连边$(X_{new}, X_{near})$
• 利用CollisionFree方法检测该边是否与地图边界及其内障碍物碰撞
  • 如果没有碰撞，则将成功完成一次空间搜索拓展
  • 如果碰撞，重新构建
• 重复上述过程，直至达到目标位置

节点扩展过程如下图所示：

2.2 基于概率的RRT算法

基于概率的RRT算法，在随机树的扩展的步骤中引入一个概率概率p，根据概率p的值来选择树的生长方向是随机生长还是朝向目标位置生长。引入向目标生长的机制可以加速路径搜索的收敛速度。算法如下图所示：

基于概率的RRT算法和Basic RRT算法的主要区别在于引入向目标生长的机制，即ChooseTarget()函数。

2.3 RRT Connect算法

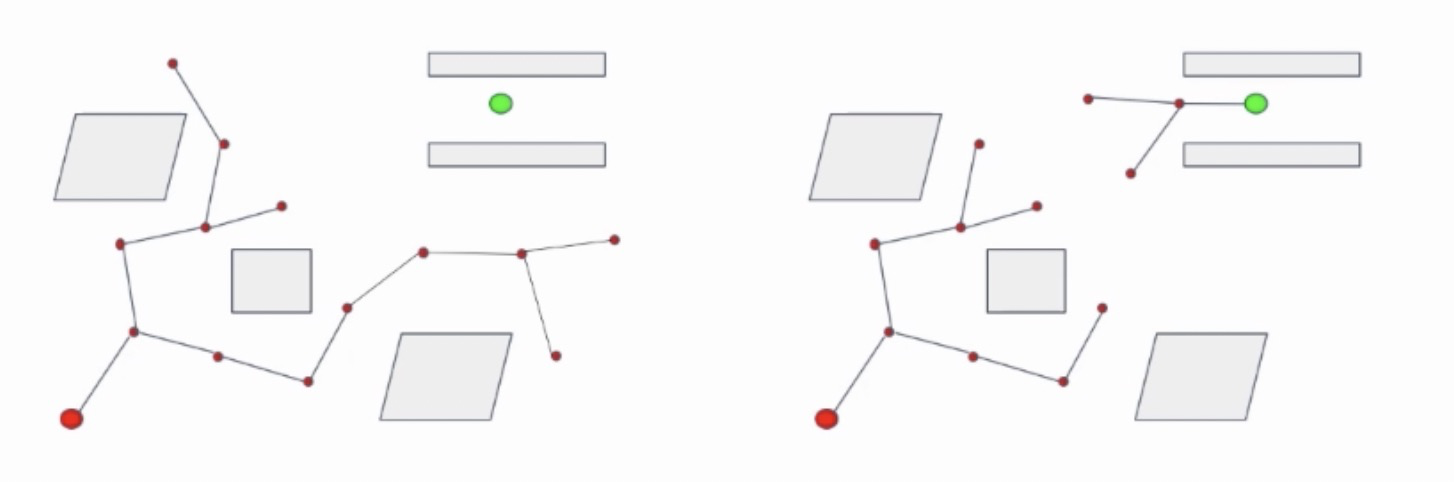
RRT-Connect分别以起点和目标点为根节点生成两棵树进行双向扩展，当两棵树建立连接时可认为路径规划成功。通过一次采样得到一个采样点，然后两棵搜索树同时向采样点方向进行扩展，加快两棵树建立连接的速度。如下图所示：

3. 代码实现

from __future__ import division
from shapely.geometry import Polygon
import yaml
import math
import shapely.geometry as geom
from shapely import affinity
import itertools
from descartes import PolygonPatch
from shapely.geometry import Point, Polygon, LineString, box
import random
from math import sqrt
import numpy as np
import time
from matplotlib import pyplot as plt


class Environment:

    def __init__(self, yaml_file=None, bounds=None):
        self.yaml_file = yaml_file
        self.environment_loaded = False
        self.obstacles = []
        self.obstacles_map = {}
        self.bounds = bounds

        if not yaml_file is None:
            if self.load_from_yaml_file(yaml_file):
                if bounds is None:
                    self.calculate_scene_dimensions()
                self.environment_loaded = True

    def bounds(self):
        return self.bounds

    def add_obstacles(self, obstacles):
        self.obstacles = self.obstacles + obstacles
        self.calculate_scene_dimensions()

    def calculate_scene_dimensions(self):
        """Compute scene bounds from obstacles."""
        points = []
        for elem in self.obstacles:
            points = points + list(elem.boundary.coords)

        mp = geom.MultiPoint(points)
        self.bounds = mp.bounds

    def load_from_yaml_file(self, yaml_file):
        f = open(yaml_file)
        self.data = yaml.safe_load(f)
        f.close()
        return self.parse_yaml_data(self.data)

    def parse_yaml_data(self, data):
        if 'environment' in data:
            env = data['environment']
            self.parse_yaml_obstacles(env['obstacles'])
            return True
        else:
            return False

    def parse_yaml_obstacles(self, obstacles):
        self.obstacles = []
        self.obstacles_map = {}
        for name, description in obstacles.items():
            if name.find("__") != -1:
                raise Exception("Names cannot contain double underscores.")
            if description['shape'] == 'rectangle':
                parsed = self.parse_rectangle(name, description)
            elif description['shape'] == 'polygon':
                parsed = self.parse_polygon(name, description)
            else:
                raise Exception("not a rectangle")
            if not parsed.is_valid:
                raise Exception("%s is not valid!" % name)
            self.obstacles.append(parsed)
            self.obstacles_map[name] = parsed

        self.expanded_obstacles = [obs.buffer(0.75 / 2, resolution=2) for obs in self.obstacles]

    def parse_rectangle(self, name, description):
        center = description['center']
        center = geom.Point((center[0], center[1]))
        length = description['length']
        width = description['width']
        # convert rotation to radians
        rotation = description['rotation']  # * math.pi/180
        # figure out the four corners.
        corners = [(center.x - length / 2., center.y - width / 2.),
                   (center.x + length / 2., center.y - width / 2.),
                   (center.x + length / 2., center.y + width / 2.),
                   (center.x - length / 2., center.y + width / 2.)]
        # print corners
        polygon = geom.Polygon(corners)
        out = affinity.rotate(polygon, rotation, origin=center)
        out.name = name
        out.cc_length = length
        out.cc_width = width
        out.cc_rotation = rotation
        return out

    def parse_polygon(self, name, description):
        _points = description['corners']
        for points in itertools.permutations(_points):
            polygon = geom.Polygon(points)
            polygon.name = name
            if polygon.is_valid:
                return polygon

    def save_to_yaml(self, yaml_file, N, start_pose, goal_region):
        yaml_dict = {}
        obstacles = {}
        rand_obstacles = self.rand_obstacles_creat(N, start_pose, goal_region)
        for i, ob in enumerate(rand_obstacles):
            ob_dict = {}
            ob_dict['shape'] = 'polygon'
            ob_dict['corners'] = [list(t) for t in list(ob.boundary.coords)]
            ob_name = "obstacle%.4d" % i
            obstacles[ob_name] = ob_dict
        yaml_dict['environment'] = {'obstacles': obstacles}

        f = open(yaml_file, 'w')
        f.write(yaml.dump(yaml_dict, default_flow_style=None))
        f.close()


class RRTPlanner():

    """Plans path using an algorithm from the RRT family.

    Contains methods for simple RRT based search, RRTstar based search and informed RRTstar based search.

    """

    def initialise(self, environment, bounds, start_pose, goal_region, object_radius, steer_distance, num_iterations, resolution, runForFullIterations):
        """Initialises the planner with information about the environment and parameters for the rrt path planers

        Args:
            environment (A yaml environment): Environment where the planner will be run. Includes obstacles.
            bounds( (int int int int) ): min x, min y, max x, and max y coordinates of the bounds of the world.
            start_pose( (float float) ): Starting x and y coordinates of the object in question.
            goal_region (Polygon): A polygon representing the region that we want our object to go to.
            object_radius (float): Radius of the object.
            steer_distance (float): Limits the length of the branches
            num_iterations (int): How many points are sampled for the creationg of the tree
            resolution (int): Number of segments used to approximate a quarter circle around a point.
            runForFullIterations (bool): If True RRT and RRTStar return the first path found without having to sample all num_iterations points.

        Returns:
            None
        """
        self.env = environment
        self.obstacles = environment.obstacles
        self.bounds = bounds
        self.minx, self.miny, self.maxx, self.maxy = bounds
        self.start_pose = start_pose
        self.goal_region = goal_region
        self.obj_radius = object_radius
        self.N = num_iterations
        self.resolution = resolution
        self.steer_distance = steer_distance
        self.V = set()
        self.E = set()
        self.child_to_parent_dict = dict()
        self.runForFullIterations = runForFullIterations
        self.goal_pose = (goal_region.centroid.coords[0])

    def RRT(self, environment, bounds, start_pose, goal_region, object_radius, steer_distance, num_iterations, resolution, drawResults, runForFullIterations, RRT_Flavour= "RRT"):
        """Returns a path from the start_pose to the goal region in the current environment using the specified RRT-variant algorithm.

        Args:
            environment (A yaml environment): Environment where the planner will be run. Includes obstacles.
            bounds( (int int int int) ): min x, min y, max x, and max y coordinates of the bounds of the world.
            start_pose( (float float) ): Starting x and y coordinates of the object in question.
            goal_region (Polygon): A polygon representing the region that we want our object to go to.
            object_radius (float): Radius of the object.
            steer_distance (float): Limits the length of the branches
            num_iterations (int): How many points are sampled for the creationg of the tree
            resolution (int): Number of segments used to approximate a quarter circle around a point.
            runForFullIterations (bool): If True RRT and RRTStar return the first path found without having to sample all num_iterations points.
            RRT_Flavour (str): A string representing what type of algorithm to use.
                               Options are 'RRT', 'RRT*', and 'InformedRRT*'. Anything else returns None,None,None.

        Returns:
            path (list<(int,int)>): A list of tuples/coordinates representing the nodes in a path from start to the goal region
            self.V (set<(int,int)>): A set of Vertices (coordinates) of nodes in the tree
            self.E (set<(int,int),(int,int)>): A set of Edges connecting one node to another node in the tree
        """
        self.env = environment

        self.initialise(environment, bounds, start_pose, goal_region, object_radius, steer_distance, num_iterations, resolution, runForFullIterations)

        x0, y0 = start_pose
        x1, y1 = goal_region.centroid.coords[0]
        start = (x0, y0)
        goal = (x1, y1)
        elapsed_time = 0
        path = []

        if start == goal:
            path = [start, goal]
            self.V.union([start, goal])
            self.E.union([(start, goal)])
        elif self.isEdgeCollisionFree(start, goal):
            path = [start, goal]
            self.V.union([start, goal])
            self.E.union([(start, goal)])
        else:
            if RRT_Flavour == "RRT":
                start_time = time.time()
                path = self.RRTSearch()
                elapsed_time = time.time() - start_time

        if path and drawResults:
            draw_results("RRT", path, self.V, self.E, environment, bounds, object_radius, resolution, start_pose, goal_region, elapsed_time)

        return path

    def RRTSearch(self):
        """Returns path using RRT algorithm.

        Builds a tree exploring from the start node until it reaches the goal region. It works by sampling random points in the map and connecting them with
        the tree we build off on each iteration of the algorithm.

        Returns:
            path (list<(int,int)>): A list of tuples/coordinates representing the nodes in a path from start to the goal region
            self.V (set<(int,int)>): A set of Vertices (coordinates) of nodes in the tree
            self.E (set<(int,int),(int,int)>): A set of Edges connecting one node to another node in the tree
        """

        path = []
        path_length = float('inf')
        tree_size = 0
        path_size = 0
        self.V.add(self.start_pose)
        goal_centroid = self.get_centroid(self.goal_region)

        for i in range(self.N):
            if(random.random() >= 1.95):
                random_point = goal_centroid
            else:
                random_point = self.get_collision_free_random_point()

            nearest_point = self.find_nearest_point(random_point)
            new_point = self.steer(nearest_point, random_point)

            if self.isEdgeCollisionFree(nearest_point, new_point):
                self.V.add(new_point)
                self.E.add((nearest_point, new_point))
                self.setParent(nearest_point, new_point)

                if self.isAtGoalRegion(new_point):
                    if not self.runForFullIterations:
                        path, tree_size, path_size, path_length = self.find_path(self.start_pose, new_point)
                        break
                    else:
                        tmp_path, tmp_tree_size, tmp_path_size, tmp_path_length = self.find_path(self.start_pose, new_point)
                        if tmp_path_length < path_length:
                            path_length = tmp_path_length
                            path = tmp_path
                            tree_size = tmp_tree_size
                            path_size = tmp_path_size
        uniPruningPath = self.uniPruning(path)
        return [path, uniPruningPath]

    def sample(self, c_max, c_min, x_center, C):
        if c_max < float('inf'):
            r= [c_max /2.0, math.sqrt(c_max**2 - c_min**2)/2.0, math.sqrt(c_max**2 - c_min**2)/2.0]
            L = np.diag(r)
            x_ball = self.sample_unit_ball()
            random_point = np.dot(np.dot(C,L), x_ball) + x_center
            random_point = (random_point[(0,0)], random_point[(1,0)])
        else:
            random_point = self.get_collision_free_random_point()
        return random_point

    def sample_unit_ball(self):
        a = random.random()
        b = random.random()

        if b < a:
            tmp = b
            b = a
            a = tmp
        sample = (b*math.cos(2*math.pi*a/b), b*math.sin(2*math.pi*a/b))
        return np.array([[sample[0]], [sample[1]], [0]])

    def find_min_point(self, nearest_set, nearest_point, new_point):
        min_point = nearest_point
        min_cost = self.cost(nearest_point) + self.linecost(nearest_point, new_point)
        for vertex in nearest_set:
            if self.isEdgeCollisionFree(vertex, new_point):
                temp_cost = self.cost(vertex) + self.linecost(vertex, new_point)
                if temp_cost < min_cost:
                    min_point = vertex
                    min_cost = temp_cost
        return min_point

    def cost(self, vertex):
        path, tree_size, path_size, path_length = self.find_path(self.start_pose, vertex)
        return path_length

    def linecost(self, point1, point2):
        return self.euclidian_dist(point1, point2)

    def getParent(self, vertex):
        return self.child_to_parent_dict[vertex]

    def setParent(self, parent, child):
        self.child_to_parent_dict[child] = parent

    def get_random_point(self):
        x = self.minx + random.random() * (self.maxx - self.minx)
        y = self.miny + random.random() * (self.maxy - self.miny)
        return (x, y)

    def get_collision_free_random_point(self):
        while True:
            point = self.get_random_point()
            buffered_point = Point(point).buffer(self.obj_radius, self.resolution)
            if self.isPointCollisionFree(buffered_point):
                return point

    def isPointCollisionFree(self, point):
        for obstacle in self.obstacles:
            if obstacle.contains(point):
                return False
        return True

    def find_nearest_point(self, random_point):
        closest_point = None
        min_dist = float('inf')
        for vertex in self.V:
            euc_dist = self.euclidian_dist(random_point, vertex)
            if euc_dist < min_dist:
                min_dist = euc_dist
                closest_point = vertex
        return closest_point

    def isOutOfBounds(self, point):
        if((point[0] - self.obj_radius) < self.minx):
            return True

        if((point[1] - self.obj_radius) < self.miny):
            return True

        if((point[0] + self.obj_radius) > self.maxx):
            return True

        if((point[1] + self.obj_radius) > self.maxy):
            return True

        return False

    def isEdgeCollisionFree(self, point1, point2):
        if self.isOutOfBounds(point2):
            return False

        line = LineString([point1, point2])
        expanded_line = line.buffer(self.obj_radius, self.resolution)
        for obstacle in self.obstacles:
            if expanded_line.intersects(obstacle):
                return False
        return True

    def steer(self, from_point, to_point):
        fromPoint_buffered = Point(from_point).buffer(self.obj_radius, self.resolution)
        toPoint_buffered = Point(to_point).buffer(self.obj_radius, self.resolution)
        if fromPoint_buffered.distance(toPoint_buffered) < self.steer_distance:
            return to_point
        else:
            from_x, from_y = from_point
            to_x, to_y = to_point
            theta = math.atan2(to_y - from_y, to_x- from_x)
            new_point = (from_x + self.steer_distance * math.cos(theta), from_y + self.steer_distance * math.sin(theta))
            return new_point

    def isAtGoalRegion(self, point):
        buffered_point = Point(point).buffer(self.obj_radius, self.resolution)
        intersection = buffered_point.intersection(self.goal_region)
        inGoal = intersection.area / buffered_point.area
        return inGoal >= 0.5

    def euclidian_dist(self, point1, point2):
        return math.sqrt((point2[0] - point1[0])**2 + (point2[1] - point1[1])**2)

    def find_path(self, start_point, end_point):
        path = [end_point]
        tree_size, path_size, path_length = len(self.V), 1, 0
        current_node = end_point
        previous_node = None
        target_node = start_point
        while current_node != target_node:
            parent = self.getParent(current_node)
            path.append(parent)
            previous_node = current_node
            current_node = parent
            path_length += self.euclidian_dist(current_node, previous_node)
            path_size += 1
        path.reverse()
        return path, tree_size, path_size, path_length

    def get_centroid(self, region):
        centroid = region.centroid.wkt
        filtered_vals = centroid[centroid.find("(")+1:centroid.find(")")]
        filtered_x = filtered_vals[0:filtered_vals.find(" ")]
        filtered_y = filtered_vals[filtered_vals.find(" ") + 1: -1]
        (x, y) = (float(filtered_x), float(filtered_y))
        return (x, y)

    def uniPruning(self, path):
        unidirectionalPath = [path[0]]
        pointTem = path[0]
        for i in range(3, len(path)):
            if not self.isEdgeCollisionFree(pointTem, path[i]):
                pointTem = path[i-1]
                unidirectionalPath.append(pointTem)
        unidirectionalPath.append(path[-1])
        return unidirectionalPath


def plot_environment(env, bounds=None, figsize=None):
    if bounds is None and env.bounds:
        minx, miny, maxx, maxy = env.bounds
    elif bounds:
        minx, miny, maxx, maxy = bounds
    else:
        minx, miny, maxx, maxy = (-10,-5,10,5)

    max_width, max_height = 12, 5.5
    if figsize is None:
        width, height = max_width, (maxy-miny)*max_width/(maxx-minx)
        if height > 5:
            width, height = (maxx-minx)*max_height/(maxy-miny), max_height
        figsize = (width, height)
    f = plt.figure(figsize=figsize)
    ax = f.add_subplot(111)
    for i, obs in enumerate(env.obstacles):
        patch = PolygonPatch(obs, fc='blue', ec='blue', alpha=0.5, zorder=20)
        ax.add_patch(patch)

    plt.xlim([minx, maxx])
    plt.ylim([miny, maxy])
    ax.set_aspect('equal', adjustable='box')
    return ax


def plot_line(ax, line):
    x, y = line.xy
    ax.plot(x, y, color='gray', linewidth=1, solid_capstyle='butt', zorder=1)


def plot_poly(ax, poly, color, alpha=1.0, zorder=1):
    patch = PolygonPatch(poly, fc=color, ec="black", alpha=alpha, zorder=zorder)
    ax.add_patch(patch)


def draw_results(algo_name, path, V, E, env, bounds, object_radius, resolution, start_pose, goal_region, elapsed_time):
    """
    Plots the path from start node to goal region as well as the graph (or tree) searched with the Sampling Based Algorithms.

    Args:
        algo_name (str): The name of the algorithm used (used as title of the plot)
        path (list<(float,float), (float,float)>): The sequence of coordinates traveled to reach goal from start node
        V (set<(float, float)>): All nodes in the explored graph/tree
        E (set<(float,float), (float, float)>): The set of all edges considered in the graph/tree
        env (yaml environment): 2D yaml environment for the path planning to take place
        bounds (int, int int int): min x, min y, max x, max y of the coordinates in the environment.
        object_radius (float): radius of our object.
        resolution (int): Number of segments used to approximate a quarter circle around a point.
        start_pose(float,float): Coordinates of initial point of the path.
        goal_region (Polygon): A polygon object representing the end goal.
        elapsed_time (float): Time it took for the algorithm to run

    Return:
        None

    Action:
        Plots a path using the environment module.
    """
    originalPath, pruningPath = path
    graph_size = len(V)
    path_size = len(originalPath)
    path_length1 = 0.0
    path_length2 = 0.0
    for i in range(len(originalPath)-1):
        path_length1 += euclidian_dist(originalPath[i], originalPath[i+1])
    for i in range(len(pruningPath)-1):
        path_length2 += euclidian_dist(pruningPath[i], pruningPath[i+1])

    title = algo_name + "\n" + str(graph_size) + " Nodes. " + str(len(env.obstacles)) + " Obstacles. Path Size: " + str(path_size) + "\n Path Length: " + str([path_length1,path_length2]) + "\n Runtime(s)= " + str(elapsed_time)

    env_plot = plot_environment(env, bounds)
    env_plot.set_title(title)
    plot_poly(env_plot, goal_region, 'green')
    buffered_start_vertex = Point(start_pose).buffer(object_radius, resolution)
    plot_poly(env_plot, buffered_start_vertex, 'red')

    for edge in E:
        line = LineString([edge[0], edge[1]])
        plot_line(env_plot, line)

    plot_path(env_plot, originalPath, object_radius,'black')
    plot_path(env_plot, pruningPath, object_radius,'red')


def euclidian_dist(point1, point2):
    return sqrt((point2[0] - point1[0])**2 + (point2[1] - point1[1])**2)


def plot_path(env_plot, path, object_radius,colorset):
    # Plots path by taking an enviroment plot and ploting in red the edges that form part of the path
    line = LineString(path)
    x, y = line.xy
    env_plot.plot(x, y, color=colorset, linewidth=3, solid_capstyle='round', zorder=1)


if __name__ == '__main__':
    environment = Environment('bugtrap.yaml')
    bounds = (-2, -3, 12, 8)
    start_pose = (2, 2.5)
    goal_region = Polygon([(10, 5), (10, 6), (11, 6), (11, 5)])
    object_radius = 0.3
    steer_distance = 0.3
    num_iterations = 10000
    resolution = 3
    drawResults = True
    runForFullIterations = False

    sbpp = RRTPlanner()
    path = sbpp.RRT(environment, bounds, start_pose, goal_region, object_radius, steer_distance, num_iterations,
                    resolution, drawResults, runForFullIterations)
    plt.show()

参考：https://github.com/hichenway/sampling-based-path-planning

4. 总结和讨论

• 优点
  • 快，因为它是随机采样，不需要对空间中所有的点都进行搜索
  • 不需要对障碍物空间进行精确建模，因为在碰撞检测时它只需要知道给定节点是否为障碍物就可以，而不需要知道障碍物的范围、形状、大小和精确的模型表示
  • 在多维空间中更具优势，维数越高，节点状态就越多，对于传统路径规划方法，很容易导致维数灾难，而RRT为随机采样，只需要随机更多的维数，而不需要采样空间中的每一个状态，因此维数的升高对RRT的效率并不会有太大的影响
• 局限性
  • 最显著的一点就是，因为RRT采样的随机性，其得到的路径有很多冗余的节点，增加了路径的长度。最常用也是最简单的优化方法就是剪枝，裁剪掉不必要的节点

5. 参考

• sampling-based-path-planning
• Python实现-RRT-Rapidly-exploring Random Tree-快速搜索随机树
• 路径规划 | 随机采样算法：PRM、RRT、RRT-Connect、RRT*
• 基于采样的运动规划算法-RRT(Rapidly-exploring Random Trees)