1. 概述

PRM (Probabilistic Roadmaps)是一种基于图搜索的方法，它将连续空间转换成离散空间，再利用A*等搜索算法在路线图上寻找路径的一种方法。其一共分为两个步骤：学习阶段和查询阶段。

2. 算法详解

2.1 学习阶段

学习阶段的主要目标是在空间中按照一定分布（如均匀分布）采样N个点，利用碰撞检测等手段去除存在障碍物内的点，在利用线段将点与点进行连线，图下图所示：

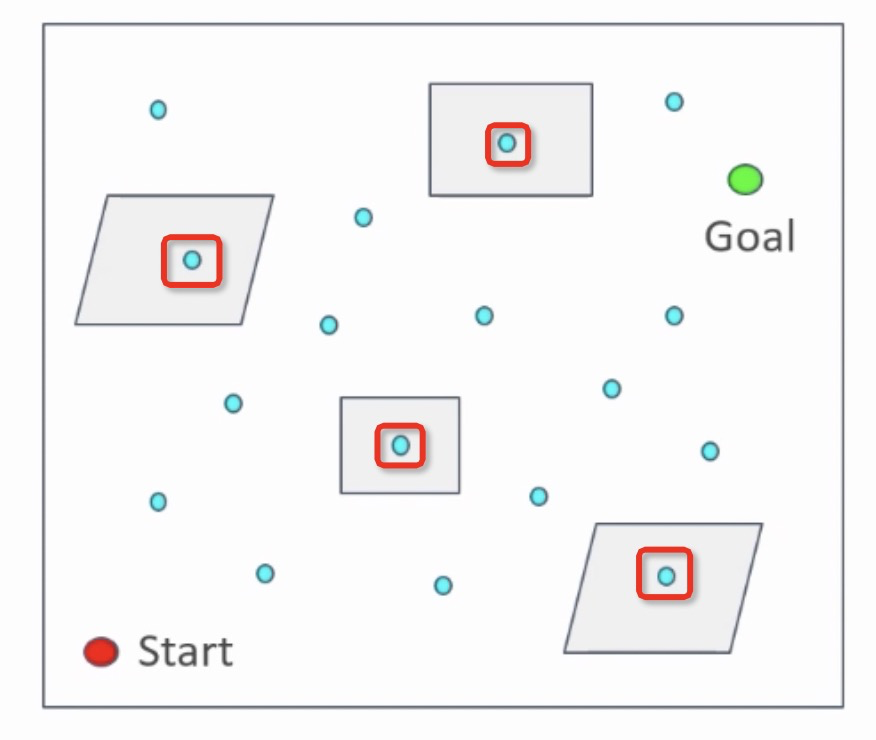
其中，蓝色的点为采样点，灰色区域为障碍物区域，红色框内的蓝色点为移除点。

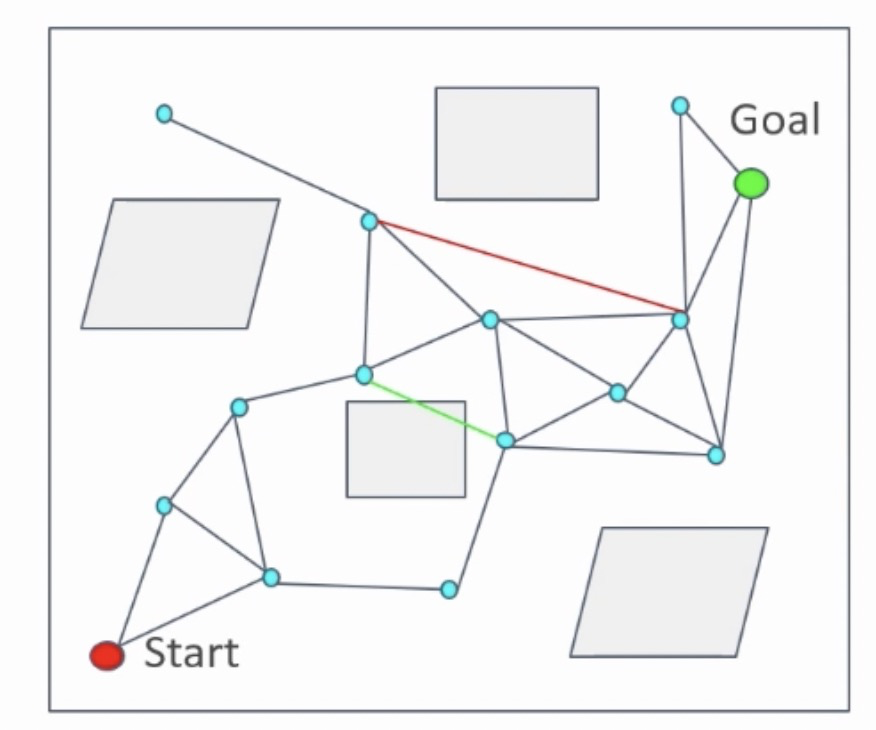
如下图所示，点与点的连接的准则：

起始和终点节点要被连接到网络中
被连接的两个点之间满足一定距离约束，例如最近邻的几个点；此处，如果没有这个约束的话，最糟糕的情况是得到了全连通图，使得后期路径规划运行时间增加
如果两个点之间的连线经过障碍物，则这条线段不可连接

2.2 查询阶段

查询阶段的主要目标是在学习阶段构建的图中，基于起始和终点节点，寻找最短路径，常用的算法是采用A*等算法。此时，再利用A*算法，搜索过程会提升很大的性能。原因在于，PRM得到的图数据结构的复杂度远远低于直接将空间进行数据建模。如下图所示：

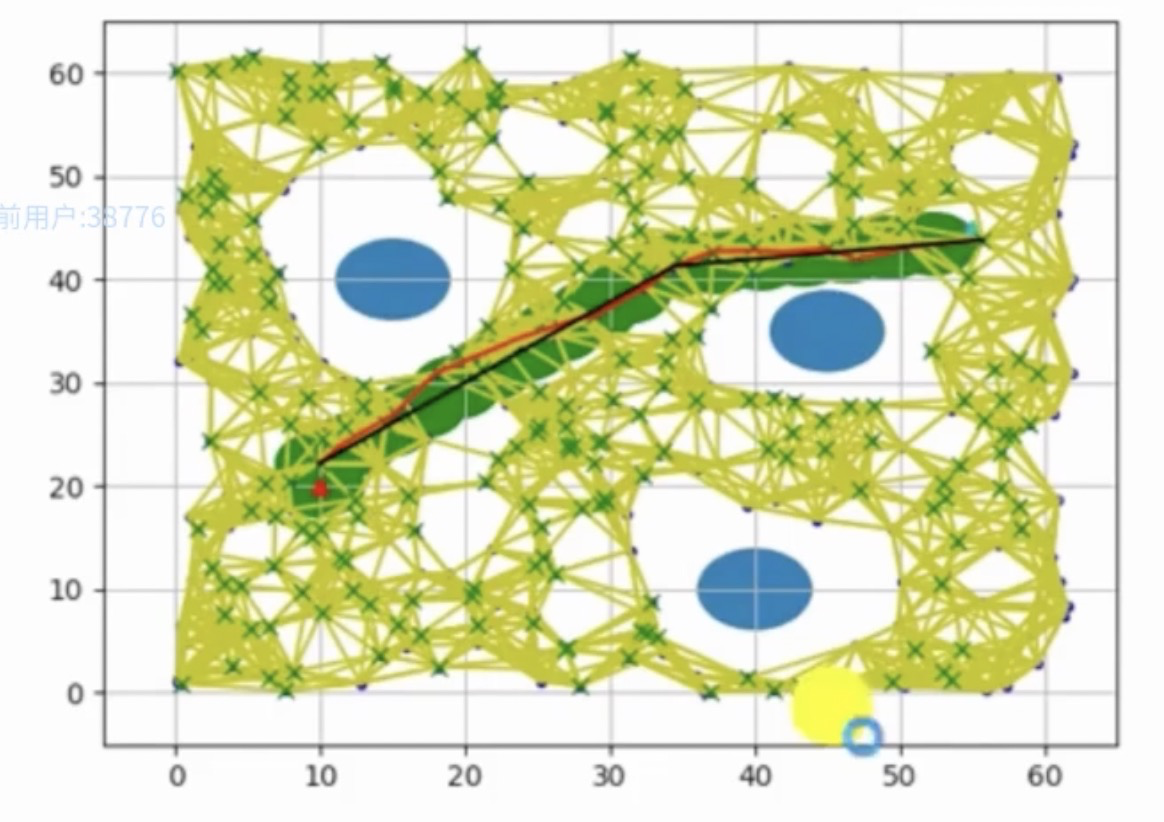
其中，红色的线段就是寻找的路径。

2.3 基于Lazy collision-checking的PRM算法

前文讲述的PRM算法，在学习阶段需要对所有的节点和节点之间的连线与障碍物进行碰撞检测，然后将碰撞的节点和边删除。当空间内采样点数量较大时，学习阶段很耗时。为了提升计算效率，基于Lazy collision-checking的PRM算法被提出来了。它的主要思想是在学习阶段，不进行碰撞检测，在查询阶段进行路径搜索时，将不可行的路段和节点再进行删除，重新进行规划。如下图所示：

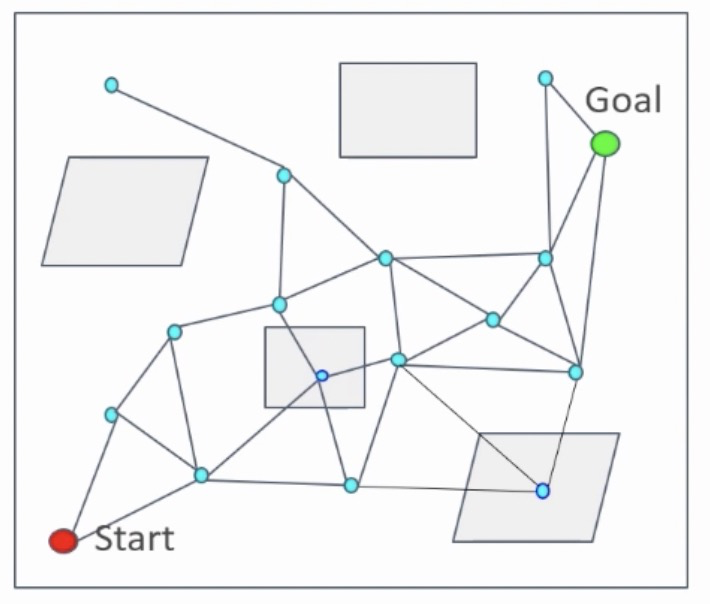
图中描述为在学习阶段随机采样点之后，对节点仅基于距离约束进行图的构建，此时不再考虑与障碍物的碰撞。图中蓝色的节点是不可行节点。基于该图结构，进行如下图所示的路径搜索，如下图红色线段所示。

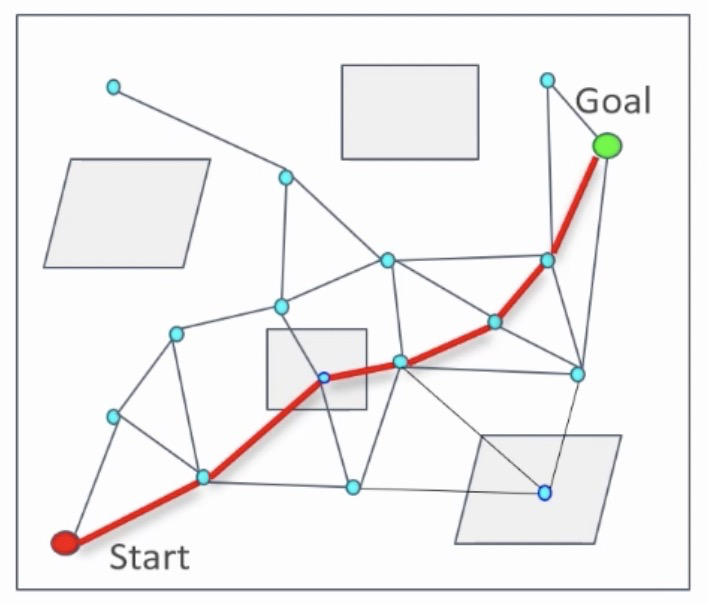
图中描述了基于上图中构建的图数据结构进行的路径搜索结果。很明显，红色的路径是不可通行路径，因为中间有节点落在障碍物区域内。此时，对图中与障碍物碰撞的节点和边进行删除，得到新的图数据结构，再运行路径搜索，如下图所示：

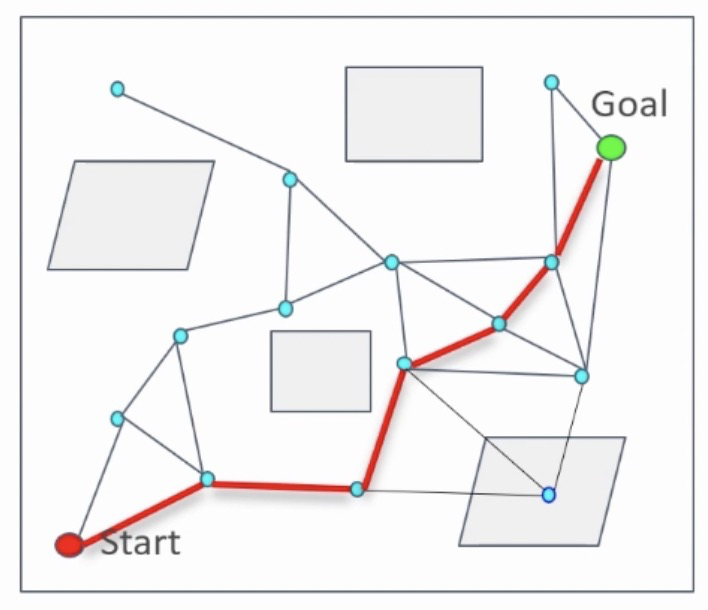
3. 代码实现

import math
from PIL import Image
import numpy as np
import networkx as nx
import copy

STAT_OBSTACLE = '#'
STAT_NORMAL = '.'


class RoadMap():

    def __init__(self, img_file):
        test_map = []
        img = Image.open(img_file)
        img_gray = img.convert('L')
        img_arr = np.array(img_gray)
        img_binary = np.where(img_arr < 127, 0, 255)
        for x in range(img_binary.shape[0]):
            temp_row = []
            for y in range(img_binary.shape[1]):
                status = STAT_OBSTACLE if img_binary[x, y] == 0 else STAT_NORMAL
                temp_row.append(status)
            test_map.append(temp_row)

        self.map = test_map
        self.cols = len(self.map[0])
        self.rows = len(self.map)

    def is_valid_xy(self, x, y):
        if x < 0 or x >= self.rows or y < 0 or y >= self.cols:
            return False
        return True

    def not_obstacle(self, x, y):
        return self.map[x][y] != STAT_OBSTACLE

    def EuclidenDistance(self, xy1, xy2):
        """两个像素点之间的欧几里得距离"""
        dis = 0
        for (x1, x2) in zip(xy1, xy2):
            dis += (x1 - x2) ** 2
        return dis ** 0.5

    def ManhattanDistance(self, xy1, xy2):
        """两个像素点之间的曼哈顿距离"""
        dis = 0
        for x1, x2 in zip(xy1, xy2):
            dis += abs(x1 - x2)
        return dis

    def check_path(self, xy1, xy2):
        """碰撞检测 两点之间的连线是否经过障碍物"""
        steps = max(abs(xy1[0] - xy2[0]), abs(xy1[1] - xy2[1]))
        xs = np.linspace(xy1[0], xy2[0], steps + 1)
        ys = np.linspace(xy1[1], xy2[1], steps + 1)
        for i in range(1, steps):
            if not self.not_obstacle(math.ceil(xs[i]), math.ceil(ys[i])):
                return False

        return True

    def plot(self, path):
        out = []
        for x in range(self.rows):
            temp = []
            for y in range(self.cols):
                if self.map[x][y] == STAT_OBSTACLE:
                    temp.append(0)
                elif self.map[x][y] == STAT_NORMAL:
                    temp.append(255)
                elif self.map[x][y] == '*':
                    temp.append(127)
                else:
                    temp.append(255)
            out.append(temp)
        for x, y in path:
            out[x][y] = 127
        out = np.array(out)
        img = Image.fromarray(np.uint8(out))
        img.show()


def path_length(path):
    """计算路径长度"""
    l = 0
    for i in range(len(path) - 1):
        x1, y1 = path[i]
        x2, y2 = path[i + 1]
        if x1 == x2 or y1 == y2:
            l += 1.0
        else:
            l += 1.4
    return l


class PRM(RoadMap):

    def __init__(self, img_file, **param):
        RoadMap.__init__(self, img_file)

        self.num_sample = param['num_sample'] if 'num_sample' in param else 100
        self.distance_neighbor = param['distance_neighbor'] if 'distance_neighbor' in param else 100
        self.G = nx.Graph()

    def learn(self):
        while len(self.G.nodes) < self.num_sample:
            XY = (np.random.randint(0, self.rows), np.random.randint(0, self.cols))
            if self.is_valid_xy(XY[0], XY[1]) and self.not_obstacle(XY[0], XY[1]):
                self.G.add_node(XY)

        for node1 in self.G.nodes:
            for node2 in self.G.nodes:
                if node1 == node2:
                    continue

                dis = self.EuclidenDistance(node1, node2)
                if dis < self.distance_neighbor and self.check_path(node1, node2):
                    self.G.add_edge(node1, node2, weight=dis)

    def find_path(self, startXY=None, endXY=None):
        temp_G = copy.deepcopy(self.G)
        startXY = tuple(startXY) if startXY else (0, 0)
        endXY = tuple(endXY) if endXY else (self.rows - 1, self.cols - 1)
        temp_G.add_node(startXY)
        temp_G.add_node(endXY)
        for node1 in [startXY, endXY]:
            for node2 in temp_G.nodes:
                dis = self.EuclidenDistance(node1, node2)
                if dis < self.distance_neighbor and self.check_path(node1, node2):
                    temp_G.add_edge(node1, node2, weight=dis)

        path = nx.shortest_path(temp_G, source=startXY, target=endXY)

        return self.construct_path(path)

    def construct_path(self, path):
        out = []
        for i in range(len(path) - 1):
            xy1, xy2 = path[i], path[i + 1]
            steps = max(abs(xy1[0] - xy2[0]), abs(xy1[1] - xy2[1]))
            xs = np.linspace(xy1[0], xy2[0], steps + 1)
            ys = np.linspace(xy1[1], xy2[1], steps + 1)
            for j in range(0, steps + 1):
                out.append((math.ceil(xs[j]), math.ceil(ys[j])))
        return out


if __name__ == '__main__':
    prm = PRM('map_1.bmp', num_sample=200, distance_neighbor=200)
    prm.learn()
    path = prm.find_path()
    prm.plot(path)
    print('Path length:', path_length(path))

参考：https://github.com/chenjm1109/robotics_tutorial_for_zhihu

4. 总结和讨论

优点
- 概率完备的，即在空间中存在解，能够找到解
- 相对比于A*算法，更加高效
缺点
- 搜索到的路径是由两个点组成的线段，不利于机器人轨迹规划
- 阶段冗余，路径规划算法的目标是找到一条路径，PRM算法提出了基于学习和查询的两个阶段。其实，在学习阶段就已经构造除了路径
参数影响
- 对同一地图，采样点的数量越多，找到合理路径以及更优路径的概率就越大。但同时，采样点数量越多，计算与搜索时间也会更长
- 邻域的设置影响着连线的建立与检测。当邻域设置过小，由于连线路径太少，可能找不到解；当领域设置太大，会检测太多较远的点之间的连线，而增加耗时
- 抽样方法的完备性很弱，即使空间中存在合理的路径，由于抽样参数的设置问题，也可能无法找到路径；另外，由于抽样过程的随机性，该方法的稳定性也不好，对于同样的问题，前后两次的解也不一样，因此在严格要求稳定性的场合并不适用

5. 参考

概率路线图(PRM)方法