1. 概述

回顾Dijkstra算法，基于广度优先搜索策略来遍历空间内所有节点，最终计算出全局最优的路径。那么它的计算量就会非常大。前面我们也介绍了基于启发式的贪婪最佳优先算法，速度快，但是结果可能不是最优的。那么，如何将二者的优势结合呢，即在Dijkstra算法基础上，引入启发式策略。这就是A*算法。

2. 算法详解

A*算法的代价函数表示方程式为：$f(n) = g(n) + h(n)$，$g(n)$表示从起始节点到当前节点所需要的代价，$h(n)$表示从当前节点到目标节点所需要的代价，$f(n)$取决于$g(n)$与$h(n)$。为了对这两个值进行相加，这两个值必须使用相同的衡量单位。如果$g(n)$用小时来衡量而$h(n)$用米来衡量，那么A*将会认为$g$或者$h$太大或者太小，因而将不能得到正确的路径，同时A*算法将运行得更慢。

2.1 启发式函数

启发式函数可以控制A*的行为：

一种极端情况，如果$h(n)$是0，则只有$g(n)$起作用，此时A*演变成Dijkstra算法，这保证能找到最短路径
如果$h(n)$经常都比从n移动到目标的实际代价小（或者相等），则A*保证能找到一条最短路径。$h(n)$越小，A*扩展的结点越多，运行就得越慢
如果$h(n)$精确地等于从n移动到目标的代价，则A*将会仅仅寻找最佳路径而不扩展别的任何结点，这会运行得非常快。尽管这不可能在所有情况下发生，你仍可以在一些特殊情况下让它们精确地相等
如果$h(n)$有时比从n移动到目标的实际代价高，则A*不能保证找到一条最短路径，但它运行得更快
另一种极端情况，如果$h(n)$比$g(n)$大很多，则只有$h(n)$起作用，A*演变成BFS算法

如下图所示：

（参考：《移动机器人运动规划》）

从上述分析中得出，启发式函数$h(n)$对于A*算法的运行结合和计算速度起到关键作用。那么启发式函数的设计有如下几种：

预计算的精确启发式函数
- 构造精确启发函数的一种方法是预先计算任意一对结点之间最短路径的长度，启发式函数可以是：
  
  h(n) = h’(n, w1) + distance(w1, w2) + h’(w2, goal)
线性精确启发式算法
- 从初始点到目标的最短路径应该是一条直线
网格地图中的启发式算法
- 曼哈顿距离（Manhattan distance）
  - 两点在南北方向上的距离加上在东西方向上的距离，即D（I，J）=|XI-XJ|+|YI-YJ|，对于一个具有正南正北、正东正西方向规则布局的城镇街道，从一点到达另一点的距离正是在南北方向上旅行的距离加上在东西方向上旅行的距离因此曼哈顿距离又称为出租车距离，曼哈顿距离不是距离不变量，当坐标轴变动时，点间的距离就会不同
  - 从一个位置移动到邻近位置的最小代价D，也可以是曼哈顿距离的D倍：H(n) = D * (abs ( n.x – goal.x ) + abs ( n.y – goal.y ) )
- 欧几里得距离
  - 沿着任意角度移动（而不是网格方向），使用直线距离：h(n) = D * sqrt((n.x-goal.x)^2 + (n.y-goal.y)^2)
- Breaking ties
  - 导致低性能的一个原因来自于启发函数的ties，即当某些路径具有相同的f值的时候，它们都会被搜索（explored），尽管我们只需要搜索其中的一条
  - 为了解决这个问题，可以为启发函数添加一个附加值，附加值对于结点必须是确定性的（也就是说，不能是随机的数），而且它必须让f值体现区别，即heuristic *= (1.0 + p)，选择因子p使得p < 移动一步（step）的最小代价 / 期望的最长路径长度。假设你不希望你的路径超过1000步（step），你可以使p = 1 / 1000。添加这个附加值的结果是，A*比以前搜索的结点更少了

2.2 A*算法流程

A*算法的流程与Dijkstra算法一样，只不过计算成本函数时，f(n)由g(n)和h(n)共同确定。算法伪代码如下图所示：

（参考：《移动机器人运动规划》）

A*算法实例如下图所示：

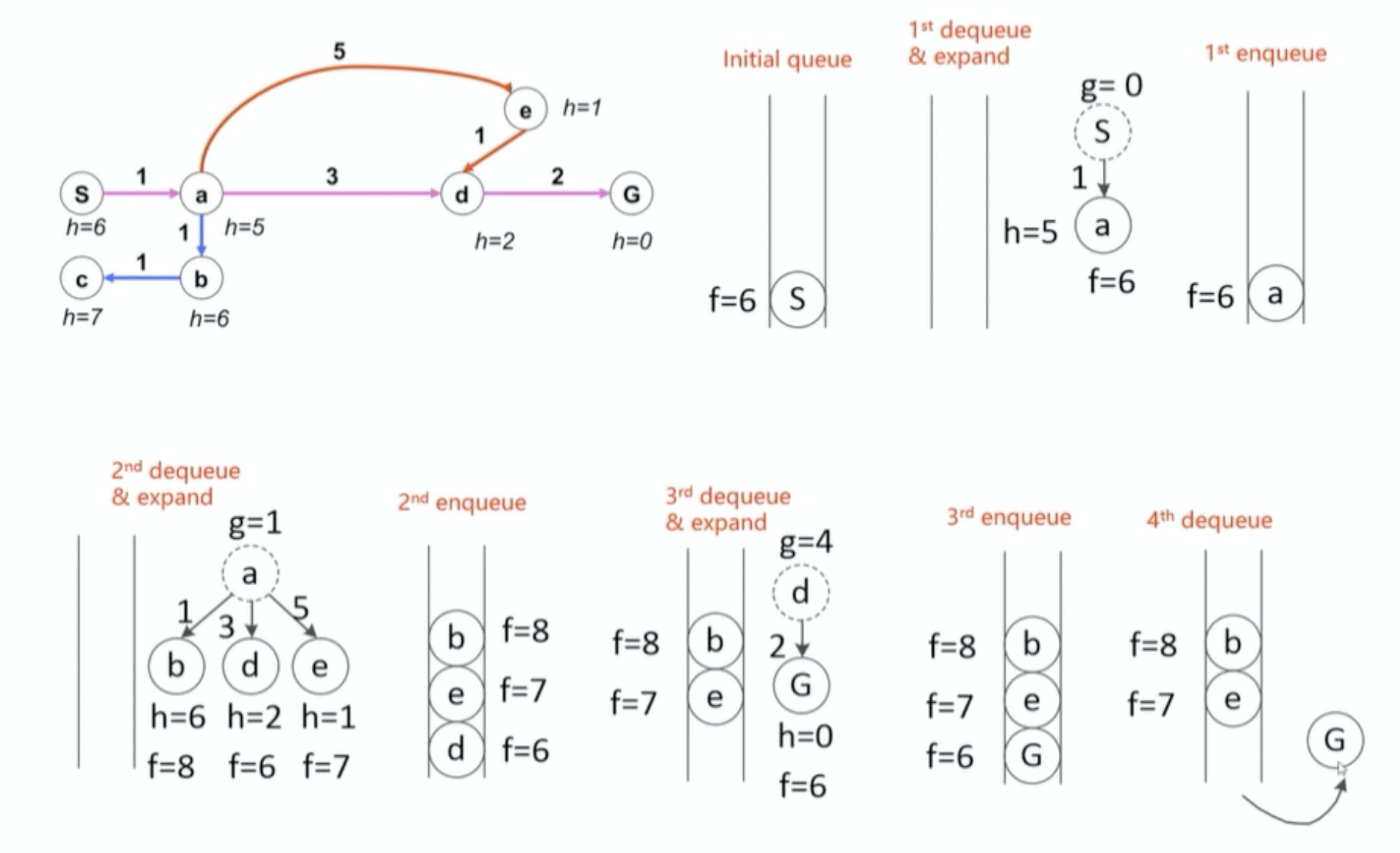
（参考：《移动机器人运动规划》）

起点为S，终点为G
初始化优先队列，仅有一个元素S
扩展S，子节点为a，那么a的成本值为1，将a放入优先队列中
扩展a，子节点包括b, d, e，那么b的成本值为8=1+1+6，b的成本值为6=1+3+2，e的成本值为7=1+5+1，可以看出d的成本值最小，将d弹出并扩展d的子节点
扩展d，d只有1个子节点，G，成本值为6=2+4+0
G节点已是目标节点，算法结束

2.3 A*算法的最优性分析

A*算法的最优性取决于启发式函数的设计。如下图所示：

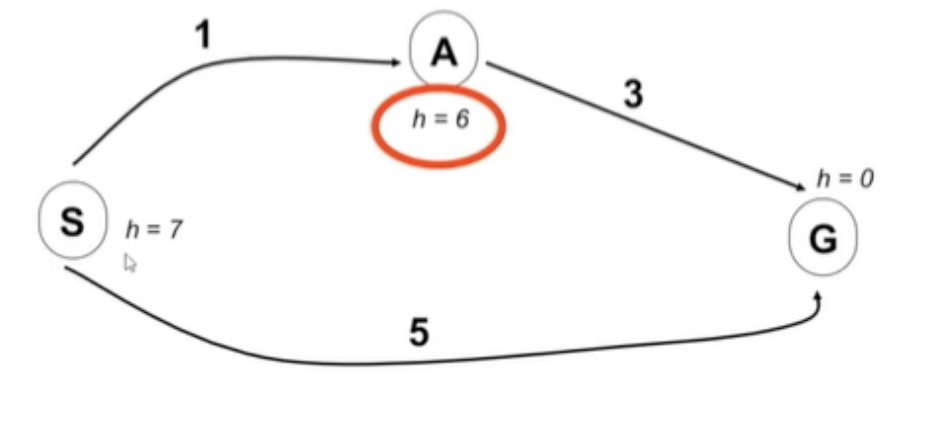
（参考：《移动机器人运动规划》）

按照A*算法的流程，我们得到路径为S->G。但是，很明显，我们发现中最有路径是S->G。那么，产生这种情况的原因是什么呢？就是在计算A节点的启发式函数值的时候，大于实际路径的数值，即6大于实际路径的数值。因此，如果启发式函数是admissible的，即$h(n) < h^{}(n)$，其中，$h_{}(n)$表示实际路径的启发式值，那么A*算法能够找到最优路径。

2.4 A*算法的优化分析

在A*算法中，如果存在多条相同f(n)的数值时，就会扩展很多节点，产生不必要的计算成本。为了解决这个问题，采用Breaking ties策略，即让多个本来具有相同的f(n)值的路径变得不同，核心思想就是对于具有相同f(n)值的路径，具有倾向性来选择其中一条。实现方法包括如下几种：

对h进行扰动，如下图公式所示：
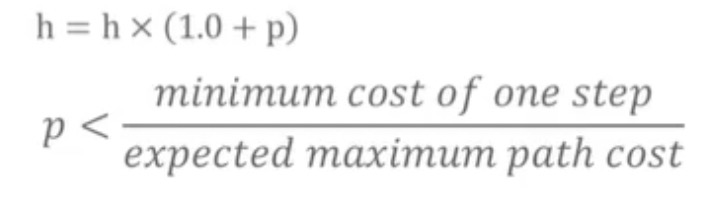
- 效果图如下图所示，其中，左图表示多条路径具有相同f(n)值的路径所扩展的节点，右图表示对相同的f(n)添加扰动，所搜索的节点：
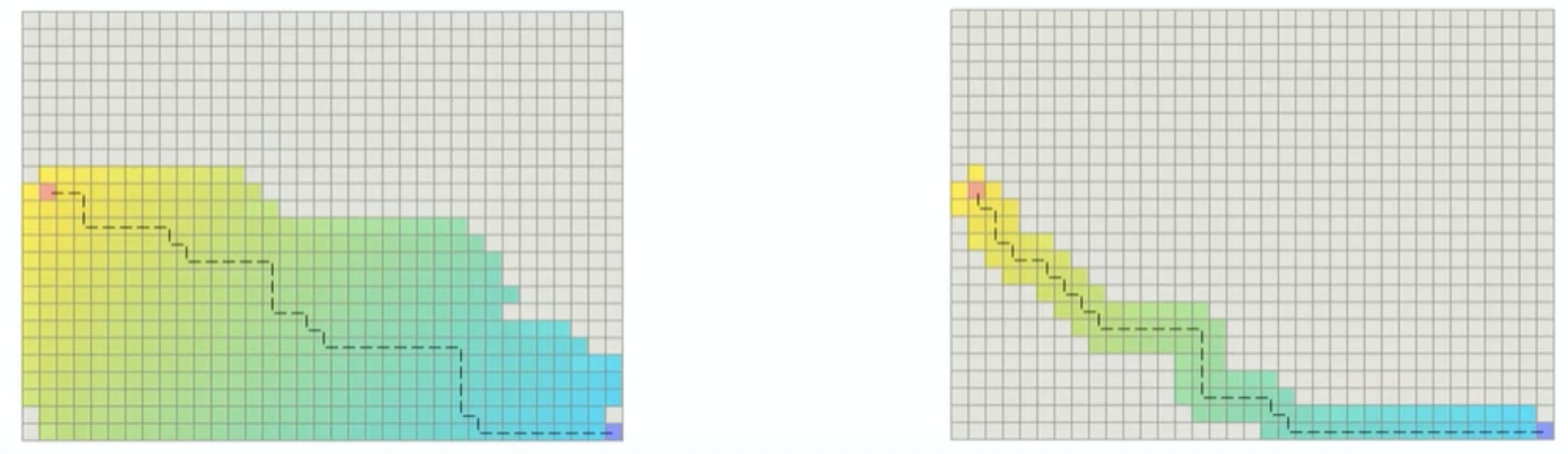
- 上述算法在工程应用中的优化，计算效率可提升20-50倍
- 此外，由于对f(n)增加了扰动，可能会导致h(n)不是精确等同于实际路径的h(n)值，打破了A*算法的最优性。但是，由于实际场景中存在大量的障碍物，这种小扰动并不会打破A*算法的最优性
对f(n)排序后，再对h(n)进行排序
添加倾向性，对于靠近起点和终点之间的连线最近的路径，如下图所示：
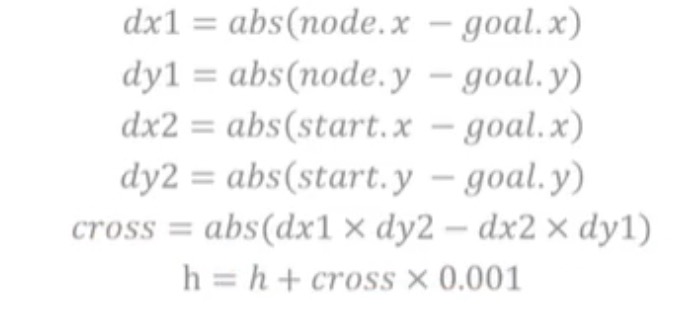
- 将倾向性的值，cross增加到h(n)中，效果如下图所示：

此外，Tie Breaker也具有如下的局限性，当含有障碍物时，找到的路径虽然也是最优的，但是对于后续应用可能不是最优的。如下图所示，找到的最优路径是折线段组成的路径，其他最优路径也包括红色曲线路径。对于后续的轨迹规划任务来说，红色曲线的路径更加具有优势，因为他更加平滑。

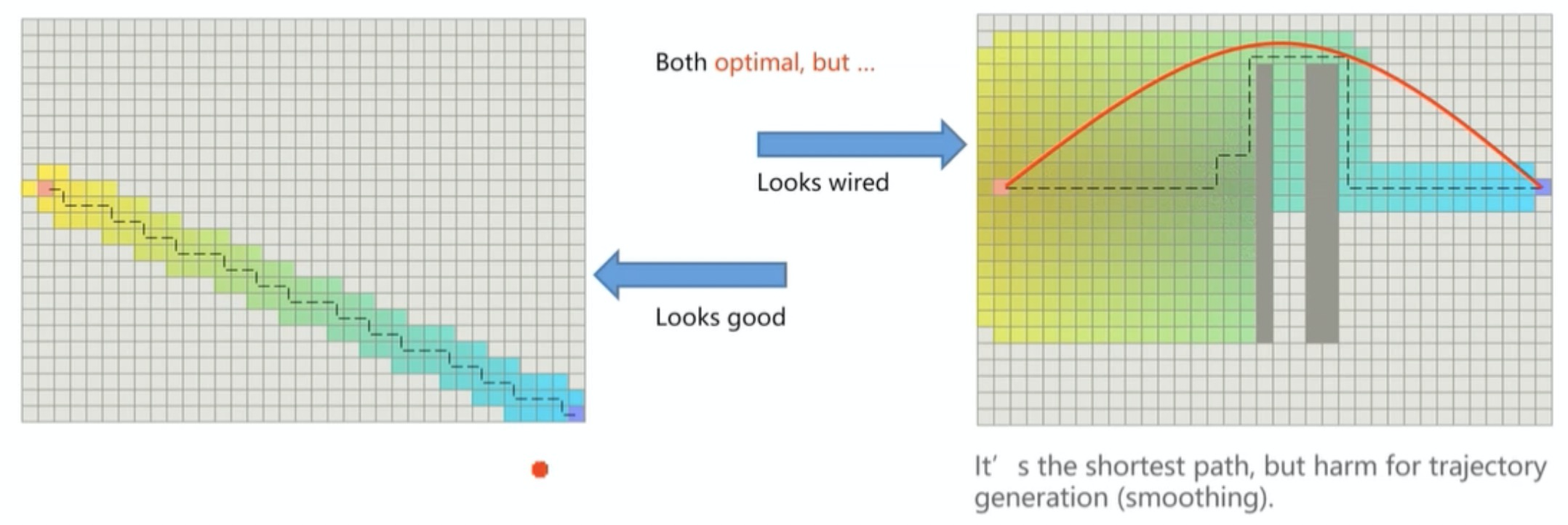
（参考：《移动机器人运动规划》）

3. 代码实现

from random import randint, seed

seed(20000)


class SearchEntry():

    def __init__(self, x, y, g_cost, f_cost=0, pre_entry=None):
        self.x = x
        self.y = y
        self.g_cost = g_cost
        self.f_cost = f_cost
        self.pre_entry = pre_entry

    def getPos(self):
        return (self.x, self.y)

    def __str__(self):
        return 'x = {}, y = {}, f = {}'.format(str(self.x), str(self.y), str(self.f_cost))


class Map():

    def __init__(self, width, height):
        self.width = width
        self.height = height
        self.map = [[0 for x in range(self.width)] for y in range(self.height)]

    def createBlock(self, block_num):
        for i in range(block_num):
            x, y = (randint(0, self.width - 1), randint(0, self.height - 1))
            self.map[y][x] = 1

    def generatePos(self, rangeX, rangeY):
        x, y = (randint(rangeX[0], rangeX[1]), randint(rangeY[0], rangeY[1]))
        while self.map[y][x] == 1:
            x, y = (randint(rangeX[0], rangeX[1]), randint(rangeY[0], rangeY[1]))
        return (x, y)

    def showMap(self):
        print("+" * (3 * self.width + 2))

        for row in self.map:
            s = '+'
            for entry in row:
                s += ' ' + str(entry) + ' '
            s += '+'
            print(s)

        print("+" * (3 * self.width + 2))


def AStarSearch(map, source, dest):

    def getNewPosition(map, locatioin, offset):
        x, y = (location.x + offset[0], location.y + offset[1])
        if x < 0 or x >= map.width or y < 0 or y >= map.height or map.map[y][x] == 1:
            return None
        return (x, y)

    def getPositions(map, location):
        offsets = [(-1, 0), (0, -1), (1, 0), (0, 1)]
        poslist = []
        for offset in offsets:
            pos = getNewPosition(map, location, offset)
            if pos is not None:
                poslist.append(pos)
        return poslist

    def calHeuristic(pos, dest):
        return abs(dest.x - pos[0]) + abs(dest.y - pos[1])

    def getMoveCost(location, pos):
        if location.x != pos[0] and location.y != pos[1]:
            return 1.4
        else:
            return 1

    def isInList(list, pos):
        if pos in list:
            return list[pos]
        return None

    def addAdjacentPositions(map, location, dest, openlist, closedlist):
        poslist = getPositions(map, location)
        for pos in poslist:
            if isInList(closedlist, pos) is not None:
                continue

            findEntry = isInList(openlist, pos)
            h_cost = calHeuristic(pos, dest)
            g_cost = location.g_cost + getMoveCost(location, pos)
            if findEntry is None:
                openlist[pos] = SearchEntry(pos[0], pos[1], g_cost, g_cost + h_cost, location)
            elif findEntry.g_cost > g_cost:
                findEntry.g_cost = g_cost
                findEntry.f_cost = g_cost + h_cost
                findEntry.pre_entry = location

    def getFastPosition(openlist):
        fast = None
        for entry in openlist.values():
            if fast is None:
                fast = entry
            elif fast.f_cost > entry.f_cost:
                fast = entry
        return fast

    openlist, closedlist = {}, {}
    location = SearchEntry(source[0], source[1], 0.0)
    dest = SearchEntry(dest[0], dest[1], 0.0)
    openlist[source] = location
    print(openlist)
    while True:
        location = getFastPosition(openlist)
        if location is None:
            print("can't find valid path")
            break

        if location.x == dest.x and location.y == dest.y:
            break

        closedlist[location.getPos()] = location
        openlist.pop(location.getPos())
        addAdjacentPositions(map, location, dest, openlist, closedlist)

    while location is not None:
        map.map[location.y][location.x] = 2
        location = location.pre_entry


if __name__ == '__main__':
    WIDTH = 10
    HEIGHT = 10
    BLOCK_NUM = 15
    map = Map(WIDTH, HEIGHT)
    map.createBlock(BLOCK_NUM)

    source = map.generatePos((0, WIDTH // 3), (0, HEIGHT // 3))
    dest = map.generatePos((WIDTH // 2, WIDTH - 1), (HEIGHT // 2, HEIGHT - 1))
    print("source:", source)
    print("dest:", dest)

    AStarSearch(map, source, dest)

    map.showMap()

（参考：python寻路算法：A* 算法实现）

4. 总结和讨论

局限性
- A*的时间复杂度是和节点数量以及起始点难度呈幂函数正相关的

算法对比

序号	算法	主要思想	优缺点
1	BFS	按照宽度向外扩展节点	可以找到最优解，但计算复杂度高
2	DFS	按照深度向外扩展节点	可以找到最优解，计算复杂度高
3	GBFS	按照宽度以一定朝向扩展节点	计算复杂度相对较低，但可能无法找到最优解
4	Dijkstra	按照一定宽度以一定成本函数值向外扩展节点，f(n) = g(n)	完备的且最优的，但计算复杂度较高
5	A*	按照一定宽度以一定成本函数值向外扩展节点，f(n) = g(n) + h(n)	依赖于启发式函数的选取，可达到完备的且最优的，但计算复杂度较高

5. 参考

python寻路算法：A* 算法实现