1. 概述
本小节介绍基于启发式的搜索算法。前文我们介绍了BFS和DFS,他们的区别主要在于节点的弹出策略,根据弹出策略的区别,分别使用了队列和栈两种数据结构,而栈和队列作为两种相当基本的容器,只将节点进入容器的顺序作为弹出节点的依据,并未考虑目标位置等因素,这就使搜索过程变得漫无目的,导致效率低下。
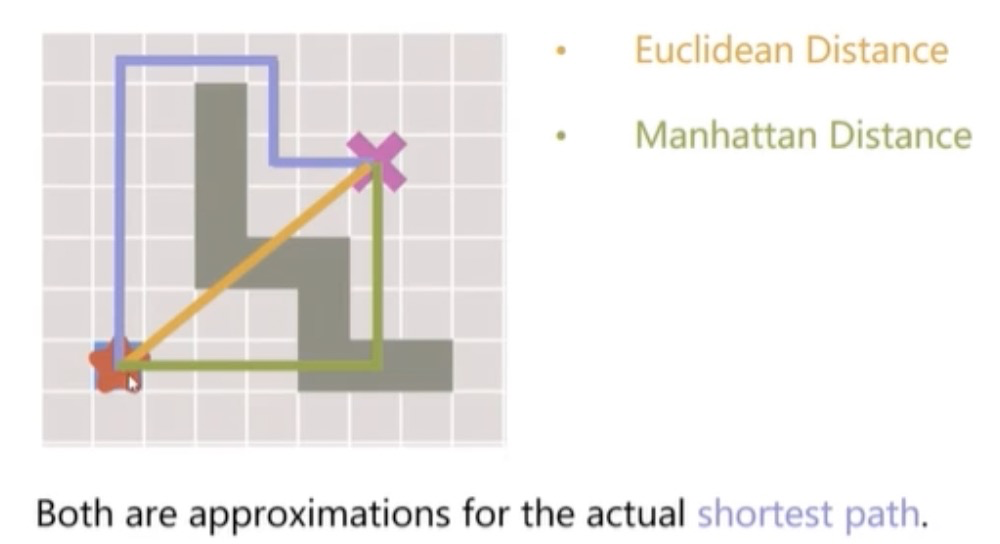
启发式搜索算法 (Heuristic Algorithm) 就是用来解决搜索效率问题的。一个Heuristic的定义就是当前位置到终点有多远的猜测。在实际使用中,从当前位置到终点的最短路径是无法得知的,除非已经完成搜索。因此,在搜索过程中,只能够猜测当前位置到终点的距离。当前,这种猜测主要基于启发式函数来实现,例如欧氏距离,曼哈顿距离等。如下图所示,黄色线段表示欧氏距离的猜测,绿色线段表示曼哈顿距离的猜测。此外,这种启发式函数在实际应用中,应该是比较容易计算的。
2. 算法详解
最佳优先搜索算法在广度优先搜索的基础上,用启发估价函数对将要被遍历到的点进行估价,然后选择代价小的进行遍历,直到找到目标节点或者遍历完所有点,算法结束。
在图搜索算法中,$f(n)$使用代价函数来作为优先级判断的标准,$f(n)$越小,优先级越高,反之优先级越低。GBFS作为一种启发式搜索算法,使用启发评估函数$f(n)$来作为代价函数,即当前节点到终点的代价,它可以指引搜索算法往终点靠近,主要用欧氏距离(Euclidean Distance)或者曼哈顿距离(Manhattan Distance)来表示。有了该代价函数,GBFS在搜索过程中极具方向性,应用在二维地图路径规划中,它的指向性或者说目的非常明显,从起点直扑终点。但是,在实际的地图中,常常会有很多障碍物,它就很容易陷入局部最优的陷阱。
算法主要思想:要实现最佳优先搜索我们必须使用一个优先队列(priority queue)来实现,通常采用一个open优先队列和一个closed集,open优先队列用来储存还没有遍历将要遍历的节点,而closed集用来储存已经被遍历过的节点。
算法时间空间复杂度分析:时间复杂度:O(b^m ),空间复杂度:O(b^m ).
算法步骤:
- 第一步:将开始结点压入优先队列中
- 第二步:从优先队列中取出优先级最高的节点为当前拓展结点,设置为已访问
- 第三步: 判断当前结点是否为目标结点,若是则输出路径搜索结束,否则进行下一步
- 第四步:访问当前结点的所有相邻子节点
- X的子节点Y不在open队列或者closed中,由估价函数计算出估价值,放入open队列中
- X的子节点Y在open队列中,且估价值优于open队列中的子节点Y,将open队列中的子节点Y的估价值替换成新的估价值并按优先值排序
- X的子节点Y在closed集中,且估价值优于closed集中的子节点Y,将closed集中的子节点Y移除,并将子节点Y加入open优先队列
- 第五步:将节点X放入closed集中
- 重复过程第二、三、四、五步直到目标节点找到,或者open为空,程序结束
3. 代码实现
1 | import networkx as nx |
4. 总结和讨论
- GBFS优点
- 搜索速度快
- GBFS的缺点
- 不一定最优(不考虑总距离)
- 容易陷入死循环
- 有可能一直沿着一条道,但是这条道到不了终点… (不完备性)
- 算法对比
| 序号 | 算法 | 主要思想 | 优缺点 |
|---|---|---|---|
| 1 | BFS | 按照宽度向外扩展节点 | 可以找到最优解,但计算复杂度高 |
| 2 | DFS | 按照深度向外扩展节点 | 可以找到最优解,计算复杂度高 |
| 3 | GBFS | 按照宽度以一定朝向扩展节点 | 计算复杂度相对较低,但可能无法找到最优解 |