1. 概述

DFS和BFS是两种搜索树和图的基本策略，一种往深处搜，一种往边上搜。 DFS常用于暴力搜索所有状态，BFS常用于搜索到达某一状态的最短路径。广度优先搜索在进一步遍历图中顶点之前，先访问当前顶点的所有邻接结点。深度优先搜索在搜索过程中访问某个顶点后，需要递归地访问此顶点的所有未访问过的相邻顶点。

2. 算法详解

2.1 深度优先搜索

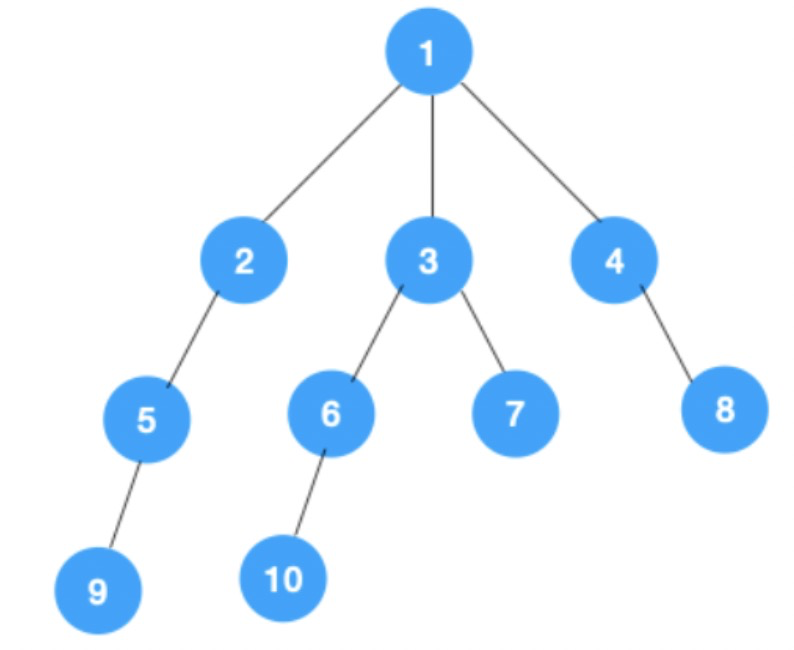
深度优先搜索策略是递归的访问此顶点的所有未访问过的相邻节点。如下图所示：

（图片参考：https://developer.aliyun.com/article/756316）

从节点1开始遍历，相邻的节点有2，3，4，先遍历节点2，再遍历节点5，然后再节点9
上图中最右侧的一条路已经走到底了，此时从节点9开始回溯到上一个节点，如果上一个节点有子节点，则在该节点处继续遍历它的子节点；如果上一个节点，没有子节点，则继续回溯。如上图所示，遍历到节点9之后，回溯到节点5，节点5没有子节点，继续回退到节点2，再回溯到节点1；此时，节点1有其他的子节点3和4，那么继续遍历3的子节点
重复上一步，直到遍历到节点10，则进行回溯，直到节点3，发现节点3有子节点7还未被访问，那么遍历节点7及其子节点
从节点7往上回溯到3，1，发现1还有节点4未遍历，所以此时沿着4，8进行遍历，最后遍历结束

2.2 广度优先搜索

广度优先遍历从图的一个未遍历的节点出发，先遍历这个节点的相邻节点，再依次遍历每个相邻节点的相邻节点。所以广度优先遍历也叫层序遍历。正如上图所示，广度优先遍历先遍历第一层（节点1），再遍历第二层（节点2，3，4），第三层（5，6，7，8），第四层（9，10）。

3. 代码实现

3.1 深度优先搜索

非递归实现

import numpy as np
from collections import defaultdict
from heapq import *


def get_DFS_data(graph, start_node):
    if len(graph) == 0:
        print("\tGraph error")
        return

    if start_node not in graph:
        print("\tStart node is not in graph, start node = ", start_node)
        return

    queue, seen_list = [], []
    queue.append(start_node)
    seen_list.append(start_node)

    while (len(queue) > 0):
        node = queue.pop()
        if node not in graph:
            print("\tNode is not in graph, node = ", node)
            return

        print("\t", node)
        subnodes = graph[node]
        for subnode in subnodes:
            if subnode not in graph:
                continue

            if subnode not in seen_list:
                queue.append(subnode)
                seen_list.append(subnode)


if __name__ == '__main__':
    graph = {
        "A": ["B", "C"],
        "B": ["A", "C", "D"],
        "C": ["A", "B", "D", "E"],
        "D": ["B", "C", "E", "F"],
        "E": ["C", "D"],
        "F": ["D"]
    }

    get_DFS_data(graph, "A")

3.2 广度优先搜索

import numpy as np
from collections import defaultdict
from heapq import *


def get_BFS_data(graph, start_node):
    if len(graph) == 0:
        print("\tGraph error")
        return

    if start_node not in graph:
        print("\tStart node is not in graph, start node = ", start_node)
        return

    queue, seen_list = [], []
    queue.append(start_node)
    seen_list.append(start_node)

    while (len(queue) > 0):
        node = queue.pop(0)
        if node not in graph:
            print("\tNode is not in graph, node = ", node)
            return

        print("\t", node)
        subnodes = graph[node]
        for subnode in subnodes:
            if subnode not in graph:
                continue

            if subnode not in seen_list:
                queue.append(subnode)
                seen_list.append(subnode)


if __name__ == '__main__':
    graph = {
        "A": ["B", "C"],
        "B": ["A", "C", "D"],
        "C": ["A", "B", "D", "E"],
        "D": ["B", "C", "E", "F"],
        "E": ["C", "D"],
        "F": ["D"]
    }

    get_BFS_data(graph, 'A')

4. 总结和讨论

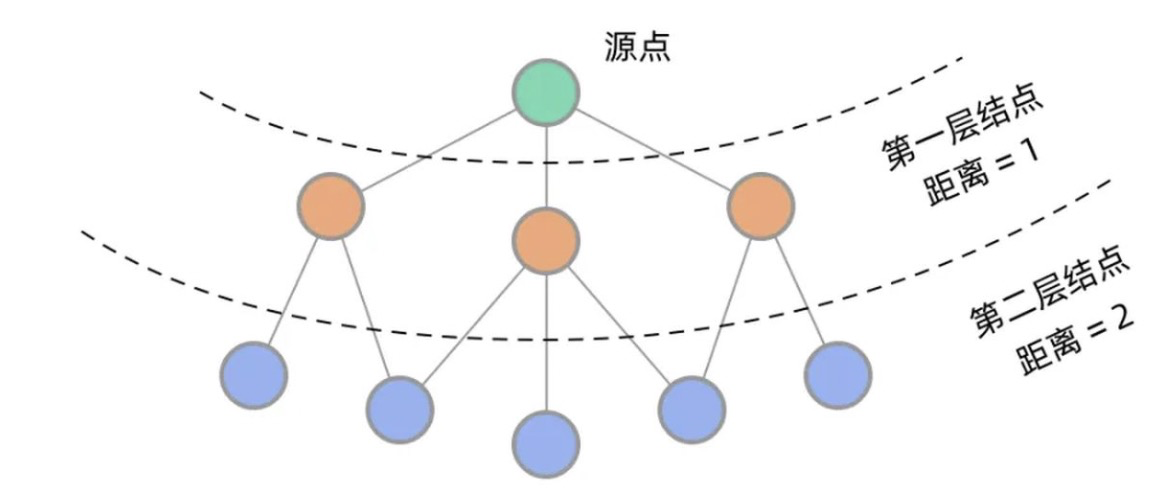
BFS和DFS可应用于最短路径问题的求解中。在一棵树中，一个结点到另一个结点的路径是唯一的，但在图中，结点之间可能有多条路径，其中哪条路最近呢？这一类问题称为最短路径问题。在图数据结构中，BFS和DFS从源点出发，一次遍历，直到遍历到目标节点结束，此时就能找到到某个点的最短路径了。

（图片参考：https://zhuanlan.zhihu.com/p/136183284）

算法对比

序号	算法	主要思想	优缺点
1	BFS	按照宽度向外扩展节点	计算复杂度高
2	DFS	按照深度向外扩展节点	计算复杂度高

路径规划（一）-BFS和DFS算法