路径规划（四）-双向Dijkstra算法

发表于 | 分类于 ，

1. 概述

Dijkstra算法是一种单向的最短路径算法，其搜索范围如下图所示。

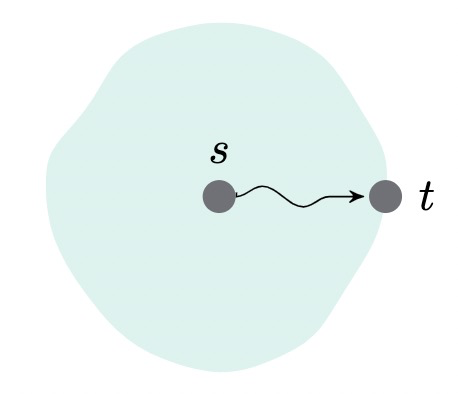
image-20201015224311183

有研究者就提出了一种优化方法，即双向Dijkstra算法。其主要思想就是从起点和终点同时开始搜索，这样应该能够提升算法效率。事实证明，在大部分情况下，双向Dijkstra算法还是要优于单向的Dijkstra算法，其搜索范围如下图所示。

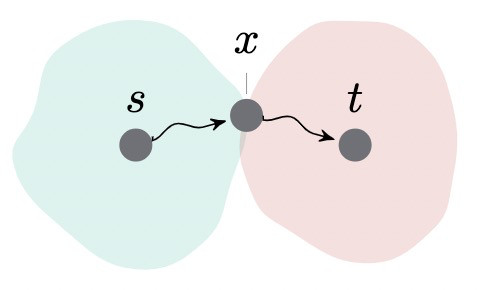
image-20201015224354382

2. 算法详解

  • 主要思想
    • 分别从路径搜索的起点s和路径搜索的终点t同时执行前向的Dijkstra算法和后向的Dijkstra算法
    • 当前向Dijkstra算法和后向Dijkstra算法相遇时，搜索结束。假设二者相遇时的节点为u，起点s到u节点的Dijkstra路径为D(s, u)，终点t到u节点的Dijkstra路径为D(t, u)，则起点s到终点t的最短路径为: D(s, u) + D(u, t)
  • 算法流程
    • 从heap中弹出节点
    • 更新当前的候选最优路径cost
    • 从当前节点广度搜索展开，更新相邻节点的权重，加入heap中
    • 最短路径搜索时我们会用到两个容器，一个堆(Heap)：维护着已经reach到的候选节点集合；一个Map:维护已经从heap中弹出的节点集合
    • PSet和PRelaxed分别表示正向搜索的Map和Heap,NSet和NRelaxed分别表示反向搜索的Map和Heap
    • 终止条件：当PSet和NSet初次相遇节点时，获得了第一条候选最优路径时，继续进行双向搜索，但这时停止向heap放入新的节点，仅用弹出当前的PRelaxed和NRelaxed的集合，最优meet节点肯定在红色背景的节点集合中。

3. 代码实现

4. 总结和讨论

5. 参考