1. 概述
- Mourikis A I, Roumeliotis S I. A multi-state constraint Kalman filter for vision-aided inertial navigation[C]//Proceedings 2007 IEEE International Conference on Robotics and Automation. IEEE, 2007: 3565-3572.
- 图像因为能够感知丰富的场景信息,因此能够提供高精度的定位结果;但是,其计算量相对较大,很难被应用于实时系统中。因此,需要从计算量和精度之间进行权衡
2. 算法详解
2.1 EKF状态量
坐标系定义:I表示IMU本体坐标系,G表示全局坐标系。
EKF的状态量定义如下:
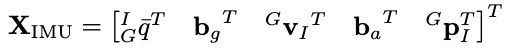
其中,$^I_G \bar{q}^T$表示G帧到I帧的旋转四元数,$^G p_I$和$^G v_I$分别表示在G帧下IMU的位置和速度,$b_g$和$b_a$分别表示陀螺仪和加速度计的bias。
IMU的误差状态定义如下:
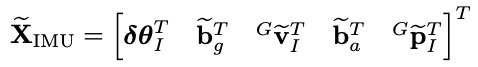
假设摄像头的姿态定义如下:
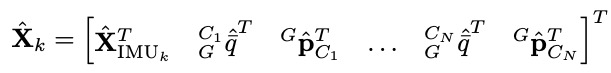
其中,$^{G_i}_G \hat{\bar{q}}^T$和$^G\hat{p}_{C_i}$表示第i个摄像头的姿态和位置。那么EKF的误差状态为:
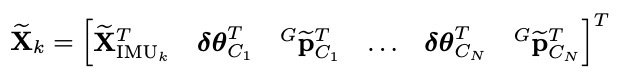
2.2 预测
2.2.1 连续时间IMU运动学
标称状态微分方程:
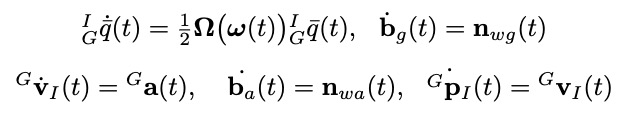
加速度计和陀螺仪传感器模型:
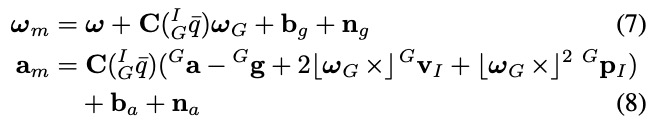
其中,考虑了科氏力对陀螺仪和加速度计的影响。
误差状态的微分方程为:
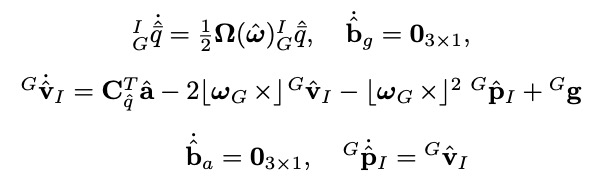
简写为:
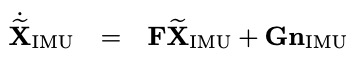
其中,$n_{IMU}$指的是系统噪声,参数均可以通过离线标定。F和G分别如下:
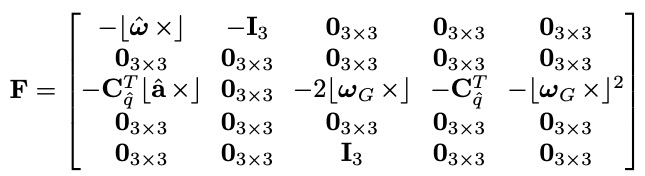
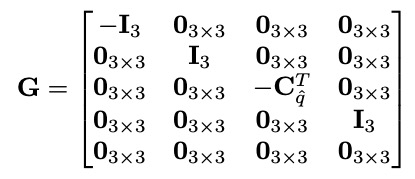
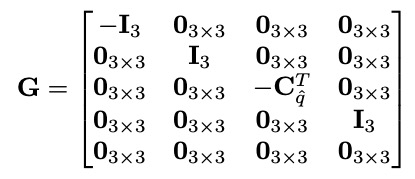
2.2.2 离散时间实现
假设IMU的采样时间为$\Delta T$,那么采用5阶Runge-Kutta数值积分来求解。定义EKF的协方差矩阵如下:
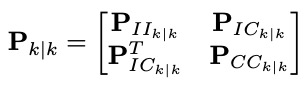
其中,$P_{II_{k|k}}$表示IMU状态的方差,维数为15x15,$P_{CC_{k|k}}$表示摄像头的姿态方差,维数为6x6,$P_{IC_{k|k}}$表示IMU和摄像头的协方差。协方差矩阵的广播方程如下:
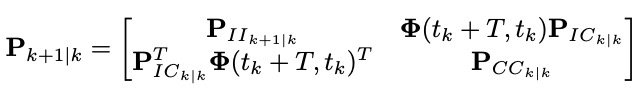
其中,$P_{II_{k+1|k}}$由下式计算:
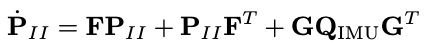
状态转移矩阵$\Phi(t_k+T, t_k)$由下式计算:
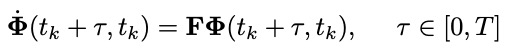
初始状态$\Phi(t_k, t_k = I_{15}$。
2.3 状态增强
当图像帧到来时,需要对当前姿态进行增广。这个时刻的相机姿态是由上一时刻的IMU propagate的结果结合外参得到的:
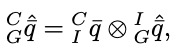
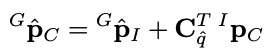
此时协方差更新方程为:
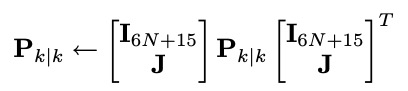
其中,J为