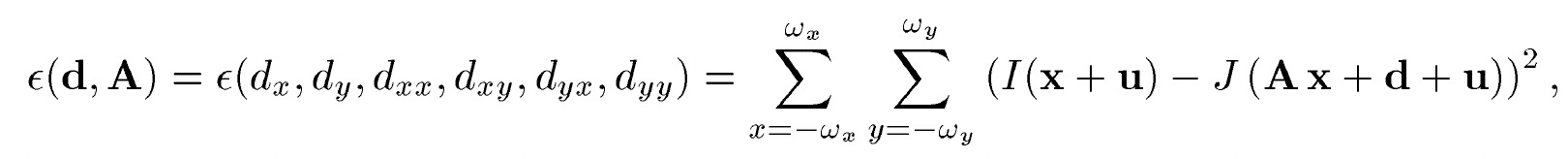1. 概述
- Lucas–Kanade光流算法是一种两帧差分的光流估计算法。它由Bruce D. Lucas 和 Takeo Kanade提出
- Lucas B D, Kanade T. An iterative image registration technique with an application to stereo vision[J]. 1981.
2. 算法详解
2.1 假设条件
- 亮度恒定,就是同一点随着时间的变化,其亮度不会发生改变。这是基本光流法的假定(所有光流法变种都必须满足),用于得到光流法基本方程
- 小运动,这个也必须满足,就是时间的变化不会引起位置的剧烈变化,这样灰度才能对位置求偏导(换句话说,小运动情况下我们才能用前后帧之间单位位置变化引起的灰度变化去近似灰度对位置的偏导数),这也是光流法不可或缺的假定
- 空间一致,一个场景上邻近的点投影到图像上也是邻近点,且邻近点速度一致。这是Lucas-Kanade光流法特有的假定,因为光流法基本方程约束只有一个,而要求x,y方向的速度,有两个未知变量。我们假定特征点邻域内做相似运动,就可以连立n多个方程求取x,y方向的速度(n为特征点邻域总点数,包括该特征点)
2.2 算法原理
相机的图像是随时间变化的。图像可以看作时间的函数:I(t)。那么,一个在t 时刻,位于(x; y) 处的像素,它的灰度可以写成I(x, y, t)。
根据上述假设条件一,我们有:
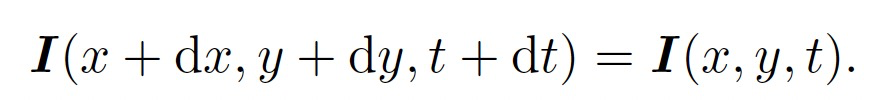
对左边进行泰勒展开,保留一阶项,得:
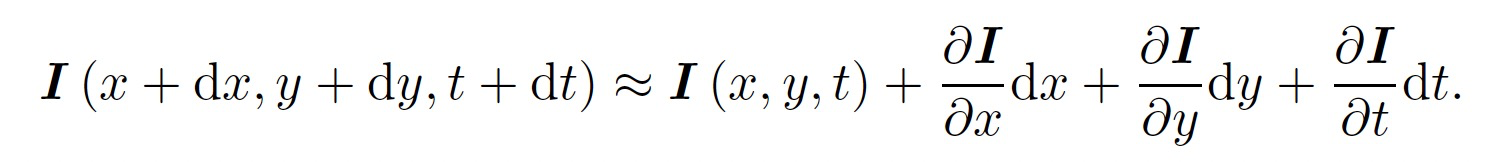
因为我们假设了灰度不变,于是下一个时刻的灰度等于之前的灰度,从而:
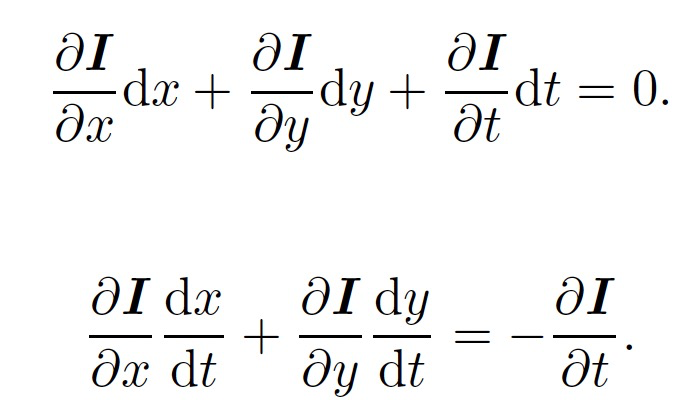
其中$\frac{dx}{dt}$像素在x轴上运动速度,而$\frac{dy}{dt}$为y 轴速度,把它们记为u; v。同时$\frac{\partial{I}}{\partial{x}}$为图像在该点处x方向的梯度,另一项则是在y 方向的梯度,记为Ix; Iy。写成矩阵形式,有:
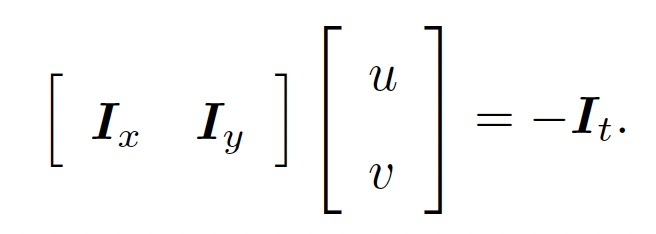
由于该方程有两个未知数,需要至少2个方程才能够解。因此,根据上述假设条件2和3,我们认为在该像素周围的一个窗口内w的像素与该像素具有相同的运动状态。因此,我们可以构建$w^2$个方程,即:
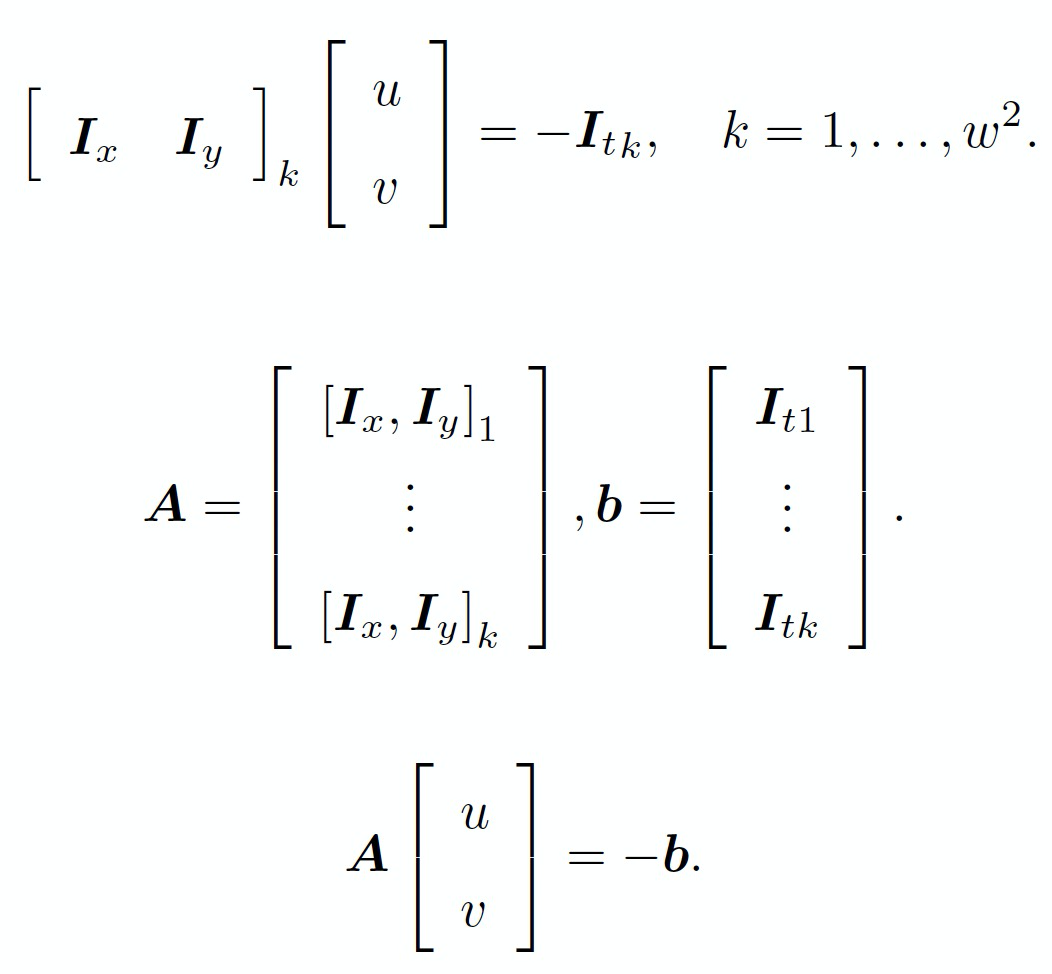
基于最小二乘求解,我们得到:
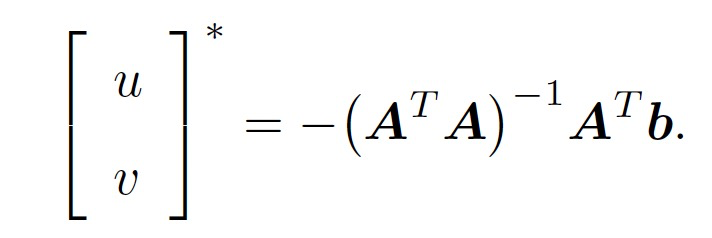
这个算法的不足在于它不能产生一个密度很高的流向量,例如在运动的边缘微小移动方面流信息会很快的褪去。它的优点在于有噪声存在的鲁棒性还是可以的。
3. 算法改进
- LK算法的约束条件即:小速度,亮度不变以及区域一致性都是较强的假设,并不很容易得到满足。如当物体运动速度较快时,假设不成立,那么后续的假设就会有较大的偏差,使得最终求出的光流值有较大的误差
- Jean-Yves Bouguet提出一种基于金字塔分层,针对仿射变换的改进Lucas-Kanade算法
- 构建图像金字塔可以解决大运动目标跟踪,也可以一定程度上解决孔径问题(相同大小的窗口能覆盖大尺度图片上尽量多的角点,而这些角点无法在原始图片上被覆盖)
- 主要思想
- 考虑物体的运动速度较大时,算法会出现较大的误差。那么就希望能减少图像中物体的运动速度。一个直观的方法就是,缩小图像的尺寸。假设当图像为400×400时,物体速度为[16 16],那么图像缩小为200×200时,速度变为[8,8]。缩小为100*100时,速度减少到[4,4]。所以光流可以通过生成 原图像的金字塔图像,逐层求解,不断精确来求得
- 上层金字塔(低分辨率)中的一个像素可以代表下层的两个
- 对于Lucas-Kanade改进算法来说,主要的步骤有三步:建立金字塔,基于金字塔跟踪,迭代过程
- Bouguet J. Pyramidal Implementation of the AÆne Lucas Kanade Feature Tracker Description of the Algorithm, Intel Corporation–Microprocessor Research Labs, 2000[J].
3.1 建立金字塔
首先需要对原始图像建立金字塔,其中原始图像位于底层,其上每一层均基于上一层进行计算。金字塔中每一层均是上一层的下采样,其计算公式为:
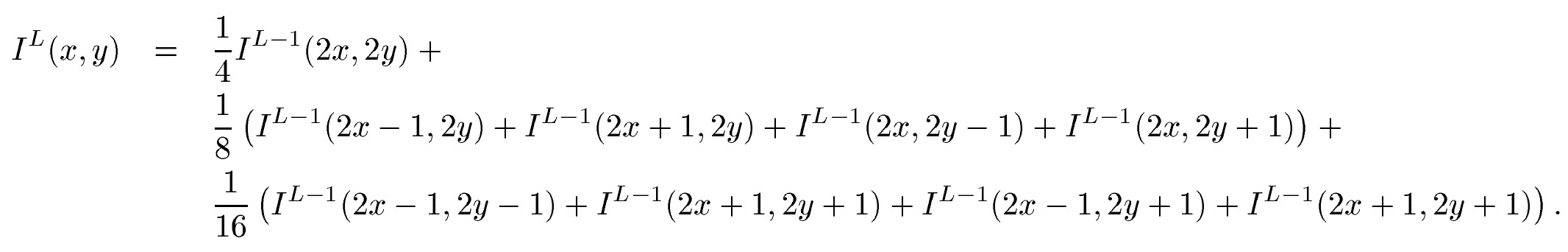
其中$I^L(x, y)$为 L 层图像中 x, y 位置所在像素点的灰度值,其相当于通过[0.25 0.5 0.25]的低通滤波器进行迭代计算。
3.2 迭代追踪
计算光流使用顶层(Lm)层开始,通过最小化每个点领域范围内的匹配误差和,得到每个顶层图像中每个点的光流,该步骤同LK光流法。假设图像的尺寸每次缩放为原来的一半,一共缩放了Lm层,则第0层为原始图像,设已知原图的位移为u,则每一层的位移可以表示为:
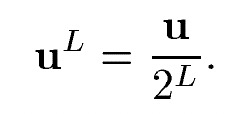
所以顶层的光流计算结果,也就是位移,反应到Lm-1层,作为该层初始时的光流值的估计g表示为:
$g^{L-1} = 2*(g^L + d^L)$.
沿着金字塔向下反馈,重复估计每一层的位移,直到最底层也就是原始图像计算像素的位移。可以理解为 准确值=估计值+残差,对于每一层L,每个点的光流的计算都是基于邻域内所有点的匹配误差和最小化。
由于顶层图像尺寸较小,其初始的光流估计量可以设置为0,即 gL = [0, 0] 。
3.3 迭代过程
介绍了对于整个金字塔迭代过程,还需要提供对于每一层的残余光流计算方法。求解光流最重要的是最小化上文提到的残差方程: