1. 概述
- 指从视觉重建中提炼出最优的3D 模型和相机参数(内参数和外参数)
- 从每一个特征点反射出来的几束光线(bundles of light rays),在我们把相机姿态和特征点空间位置做出最优的调整(adjustment) 之后,最后收束到相机光心的这个过程,简称为BA
2. 投影模型
- 相机模型也有很多啦,这里我们同样是使用最简单的一种:针孔相机模型
- 首先,把世界坐标转换到相机坐标,这里将用到相机外参数(R; t)
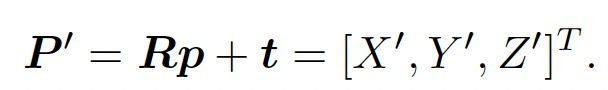
- 然后,将P′ 投至归一化平面,得到归一化坐标
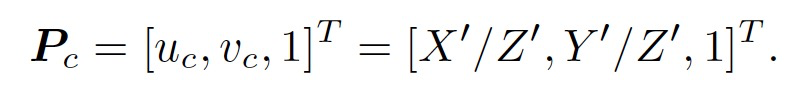
- 对归一化坐标去畸变,得到去畸变后的坐标。这里暂时只考虑径向畸变
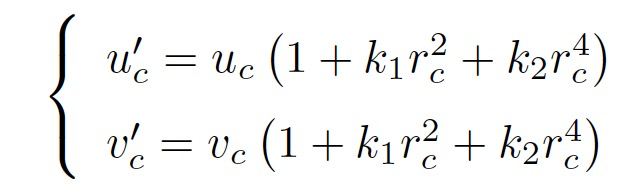
- 最后,根据内参模型,计算像素坐标
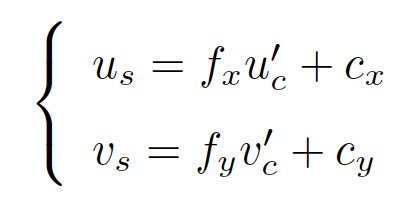
3. 观测方程参数化
观测方程为:$z = h(x, y)$,其中x表示相机的位姿,即外参R和t,李代数为$\xi$;y表示三维点p的坐标。
误差项即:$e = z - h(\xi, p)$。
对于每一个时刻进行误差计算,得到总体的代价函数为:
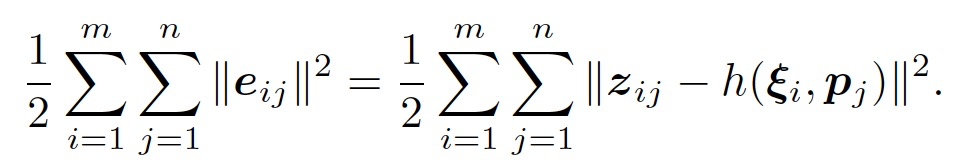
对这个最小二乘进行求解,相当于对位姿和路标同时作了调整,也就是所谓的BA。
上述式子进一步整理为如下公式:
$\arg \min \sum_{\{i, j, k\}\in X} \rho(e^T\Sigma^{-1}e)$.
其中,$\rho$为Huber函数。
为了便于计算,这里采用g2o方法,使得$e^T\Sigma^{-1}e = \rho(e^T\Sigma^{-1}e)$,
那么,$w = \frac{\rho(e^T\Sigma^{-1}e)}{e^T\Sigma^{-1}e}$.
因此,成本函数可以写成如下公式:
$\{T_i, X_j\} = \arg \min \sum_{\{i, j, k\}\in X}e^T(w\Sigma^{-1})e$.
代码实现:
1 | void CostFunction::ComputeInterVars(Eigen::Vector2d &e, Eigen::Matrix2d &weighted_info, double &weighted_e2) { |
4. BA的求解
状态量定义为:
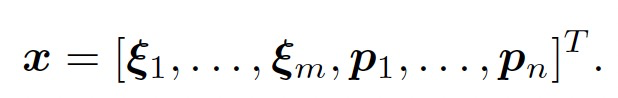
相应的,增量方程中的$\Delta x$则是对整体自变量的增量。在这个意义下,当我们给自变量一个增量时,目标函数变为:
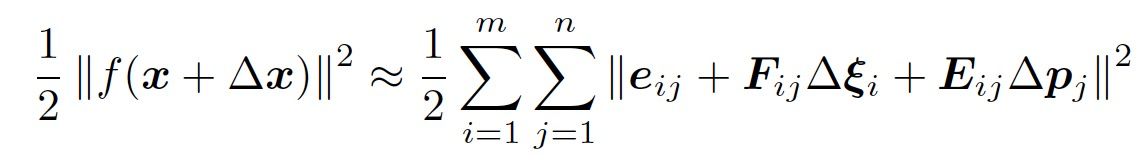
其中,$F_{ij}$和$E_{ij}$分别表示整个儿代价函数在当前状态下对相机姿态和路标坐标的偏导。详细推导如下。
(1)首先推导F
F是误差对相机姿态$\xi$的偏导矩阵。记变换到相机坐标系下的空间点坐标为P’,即:
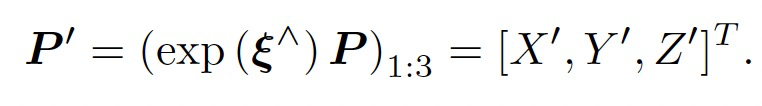
根据相机投影模型,得到:
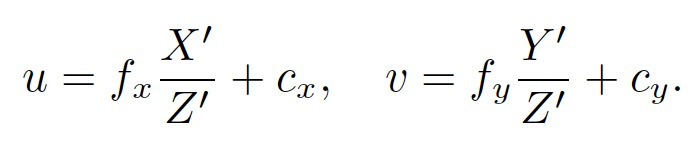
误差e可以通过u和v来求取。接下来,计算e对$\xi$的偏导。采用扰动形式求导,对$\xi$^左乘$\delta \xi$,根据导数定义可得:
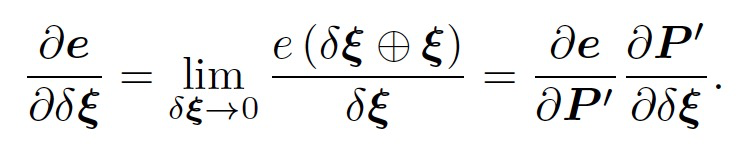
其中,第一项是误差关于投影点的导数,第二项为变换后的点关于李代数的导数。
根据投影模型,可得:
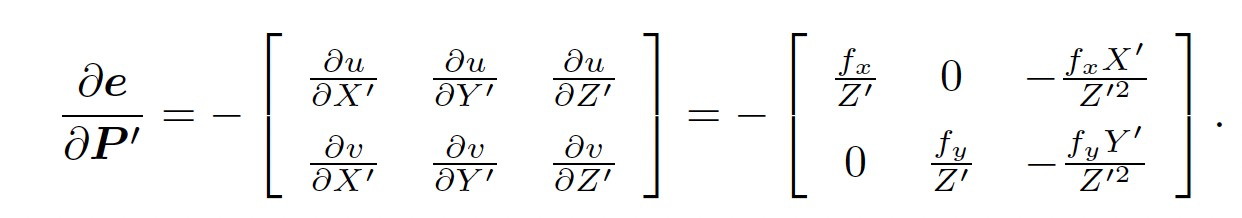
根据SE(3)上的李代数求导可得:

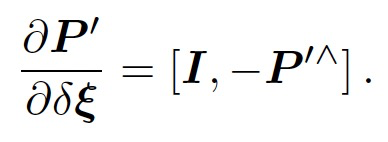
将这两项相乘,就得到了雅可比矩阵F,即:
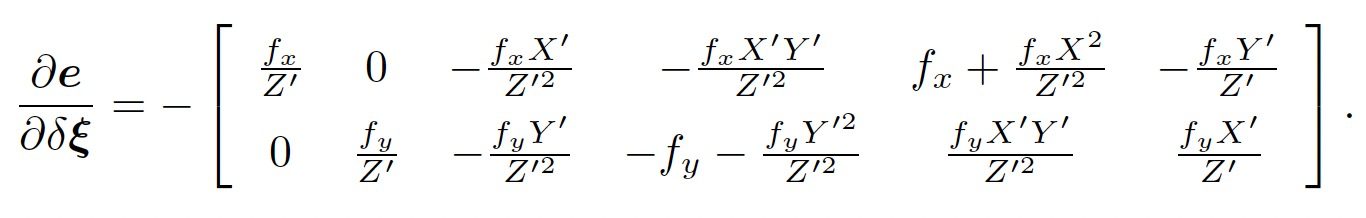
(2)推导E
根据链式法则,可得:
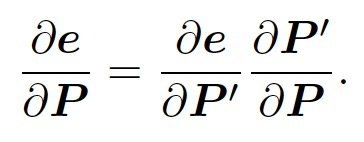
第一项已在前面推导了,第二项,按照定义
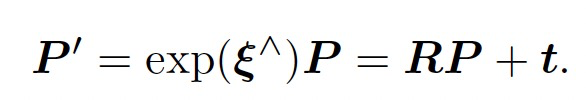
可得:
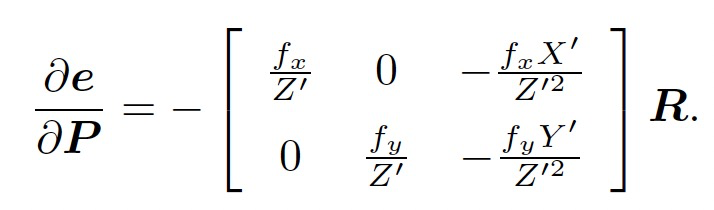
(3)代码实现
- 定义Camera类
- 位姿Sophus::SE3
- ID
- 位姿更新
- 状态量中的索引
1 | Camera::Camera(const Sophus::SE3 &pose, int id, bool isFixed) : m_Pose(pose), m_ID(id), m_Fixed(isFixed), _state_index(-1) { |
- 定义地图点类
- 三维点坐标
- ID
- 位置更新
- 状态量中的索引
1 | MapPoint::MapPoint(const Eigen::Vector3d& position, int id) : m_Positon(position), m_ID(id), _state_index(-1) { |
- 定义损失函数类
- 相机、地图点、相机内参、观测值、超参数(Hubor核参数b,信息矩阵)
- 误差对相机位姿的Jacobian矩阵JT
- 误差对地图点的Jacobian矩阵JX
- 基于Hubor核函数的成本函数计算
1 | CostFunction::CostFunction(MapPoint *map_point, Camera *camera, double fx, double fy, double cx, double cy, const Eigen::Vector2d &ob_z) |
5. 增量线性方程
无论使用Gauss-Netwon还是Levenburg-Marquadt方法求解最小二乘问题,都会求解一个关于增量的线性方程:
$H\delta x = g$.
G-N 和L-M 的主要差别在于,这里的H 是取$J^TJ$还是$J^TJ + \lambda I$的形式。由于我们把变量归类成了位姿和空间点两种,所以雅可比矩阵可以分块为:
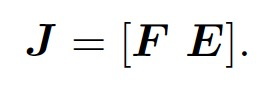
因此,我们得到:
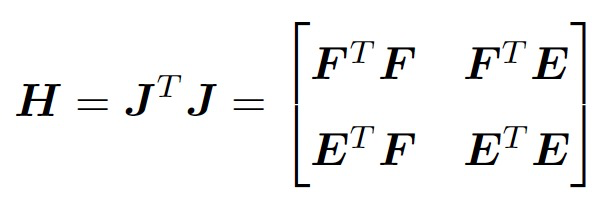
Bundle Adjustment中的H矩阵,具有特殊的稀疏结构。利用这种稀疏结构可以加速求解过程。我们这里的实现使用了舒尔补的方法求解。如下图所示:
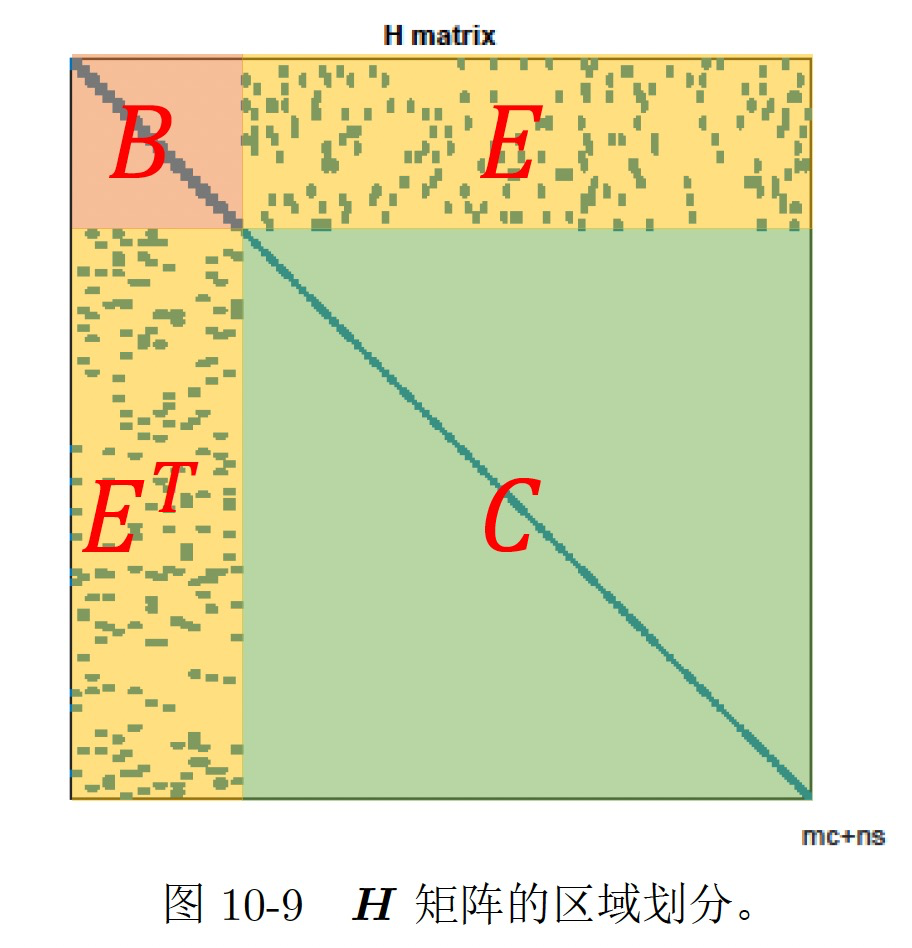
因此,线性方程组$H\delta x = g$可以写为:
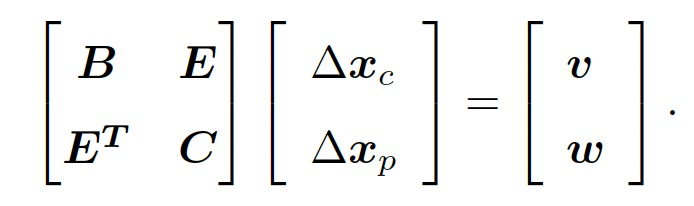
利用舒尔补消元,我们首先求解$\delta x$。
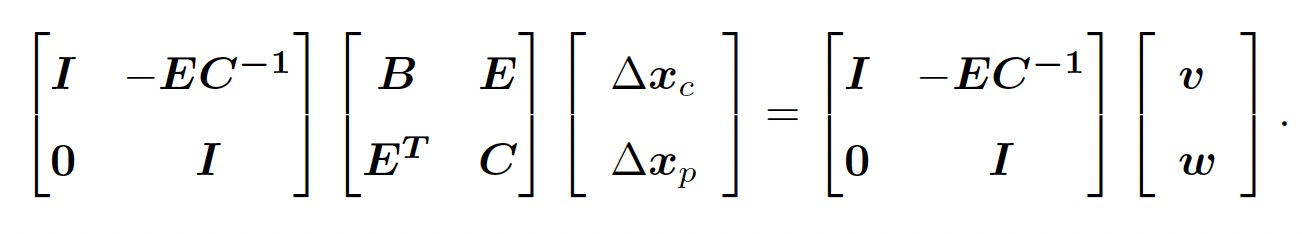
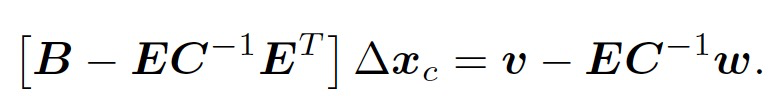
然后再去求解$\delta x_p$:
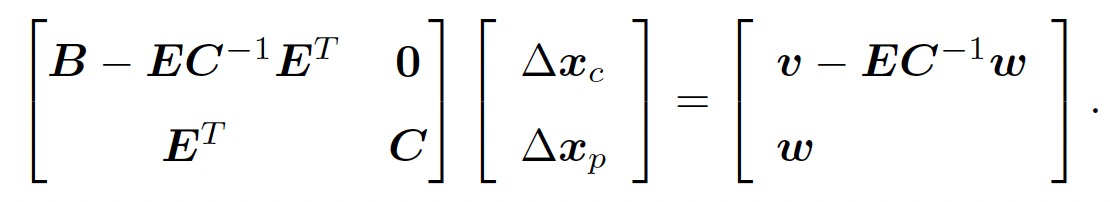
由于C 为对角块,所以$C^{-1}$容易解得。
6. 固定部分状态
对于一个Bundle Adjustment问题,我们必须固定一部分状态,或者给一部分状态一个先验。不然,就会有无穷多解。可以想象一下,一个网络的误差已经达到了最小后,可以整体在空间内任意移动,而不会对误差造成任何影响。我们只要固定这个网络中的任意1个以上的节点,其他的节点都会有确定的状态。(我们通常会把第一个位姿固定)
怎么固定呢?一种可以加一个先验约束,就是加一个先验cost function。另外一种就是直接把状态fix住,不让它参与优化就好了。 我们采用后一种方法。
7. 代码实现
- 实现思路如上所述
- 实现代码参考如下工程
- 简单介绍
- 依赖库
- Eigen3
- Sophus
- OpenCV
- 结构
- 定义几个类,分别是地图点,相机位姿,CostFunction
- 地图点和相机位姿类用来存储需要优化的状态,通过id进行标识
- CostFunction用来存储代价函数、观测,计算雅克比、残差等
- BundleAdjustment类求解BA问题
- map结构存储地图点和相机,主要是为了方便快速查找;构造地图点、相机,加入到BundleAdjustment类
- set结构存储cost function,构造cost function,加入到BundleAdjustment类
- 将所有cost function的雅克比、信息矩阵整合成大的雅克比、信息矩阵、Hassian矩阵等
- 采用LM优化算法求解最小二乘问题
- 根据id将结果取出
- 依赖库
(1)初始化BundleAdjustment类
- 设定优化算法迭代终止条件
- 最大迭代次数20
- 误差阈值1e-10
- 设置min delta
1 | void BundleAjustment::Init(int max_iters, double min_delta, double min_error, bool verbose) { |
(2)将地图点、相机和成本函数添加到BundleAdjustment类
- ID就是添加到顺序索引
1 |
|
(3)采用LM优化算法求解
- 初始化
- 确定各个矩阵的大小
- 定义状态量大小为$N_s$,相机个数为$N_c$,地图点个数为$N_m$,观测数量为$N_{cost}$,观测量大小为$N_o$
- $N_s = N_c \times 6 + N_m \times 3$,其中,6表示相机的位姿维度,即se3,3表示地图点向量维度,即三维坐标
- $N_o = N_{cost} \times 2$,其中,2表示每个Jacobian为2行
- Jacobian大小为$N_o \times N_s$
- H的大小为$N_s \times N_s$,$H = J^TJ$
- r的大小为$N_o \times 1$
- b的大小为$N_s \times 1$,$b = -J^Tr$
- $\Delta x$的大小为$N_s \times 1$
- 信息矩阵大小为$N_o \times N_o$
1 | void BundleAjustment::optimizationInit() { |
- 求H、b和误差量
- H的大小为$N_s \times N_s$,$H = J^TJ$
- r的大小为$N_o \times 1$
- b的大小为$N_s \times 1$,$b = -J^Tr$
1 |
|
- LM求解
- 计算$\mu$,首先令$\mu = \tau\max{H_{i, i}}$,其中,$\tau = 1e-8$
- $H += \mu I$
- 利用舒尔补方法和QR分解求解正规方程
- 根据求解出来的$\Delta X$状态量更新相机和地图点状态
- 再次计算H、b和误差量
- 更新LM中的参数$\mu$
- 计算超参数$\rho = \frac{F(x) - f(x + h)}{L(0) - L(h)}$
- 如果$\rho > 0$,则接受$\mu$,更新$\mu = \mu\max(\frac{1}{3}, 1 - (2\rho - 1)^3)$,$v = v\times2$
- 如果$\rho \leq 0$,则拒绝本次更新,恢复前一步的相机和地图点状态并重新计算H、b和误差,$\mu = v\times\mu$,$v = v\times2$
1 | void BundleAjustment::optimize() { |
8. 参考
- [V-SLAM] Bundle Adjustment 实现
- 《视觉SLAM十四讲》