1. 概述

将一幅图像表示为一系列的平滑图像，称为尺度空间表示，这些平滑图像可参数化表示为平滑核（用于抑制细尺度结构）的尺寸
当用一个机器视觉系统分析未知场景时，计算机没有办法预先知识图像中物体尺度，因此，我们需要同时考虑图像在多尺度下的描述，获知感兴趣物体的最佳尺度。所以在很多时候，我们会在将图像构建为一系列不同尺度的图像集，在不同的尺度中去检测我们感兴趣的特征
尺度空间的其中一个主要类型，就是线性（高斯）尺度空间。高斯尺度空间因其良好的性质而被广泛地应用

2. 尺度空间

对于给定的一幅二维图像$f(x, y)$，线性尺度空间表示是由一系列的派生信号$L(x, y; t)$组成，其中$L(x, y; t)$为$f(x, y)$与一个二维高斯核卷积而成，其中高斯核定义如下

$g(x, y; t) = \frac{1}{w\pi t}e^{-\frac{(x^2 + y^2)}{2t}}$.

因此有，

$L(x, y; t) = g(x, y; t) * f(x, y)$,

其中，$*$表示卷积操作，$t$是指定义好的尺度级别。

尺度参数$t = \sigma^2$是高斯filter的方差。当t趋于零时，g就成为了一个脉冲函数（除了零点，别处的函数值都为零），则有$L(x, y; 0) = f(x, y)$, 也就是说，位于尺度级别 t = 0 的尺度空间表示（scale-space representation）就是原图本身
随着t的增大，越来越大的filter被作用于图像f，形成平滑度越来越高的L，以至于原图中越来越多的细节被丢弃
由于每个filter的标准差为$\sigma = \sqrt{t}$, 对于位于尺度等级t的图像，远小于$\sqrt{t}$的细节很大程度上会被丢弃
并非任何低通filter都可用于生成尺度空间。可用于生成尺度空间的filter必须满足以下一点：由该平滑filter生成的粗尺度图像（高层图像）不会引入不存在于细尺度图像（低层图像）中的杂散结构。换言之，给定粗尺度图像中的任何一个区域，细尺度图像上总能找到相应的区域。这两个区域相比，粗尺度图像区域不能够有新的结构
受制于尺度空间公理，高斯卷积核是实现尺度变换的唯一线性核

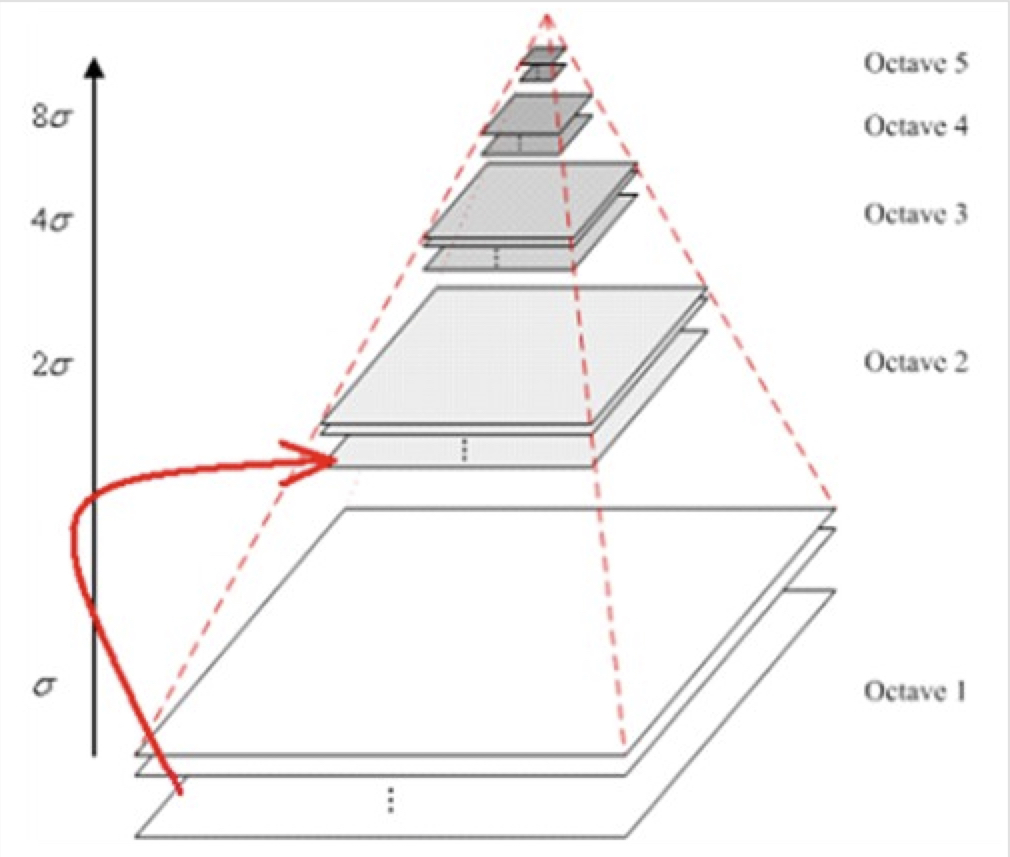
为了让尺度体现其连续性，高斯金字塔在简单降采样的基础上加上了高斯滤波
图像金字塔每层的一张图像使用不同参数做高斯模糊，使得金字塔的每层含有多张高斯模糊图像，将金字塔每层多张图像合称为一组(Octave)，金字塔每层只有一组图像，组数和金字塔层数相等，每组含有多张(也叫层Interval)图像
降采样时，高斯金字塔上一组图像的初始图像(底层图像)是由前一组图像的倒数第三张图像隔点采样得到的

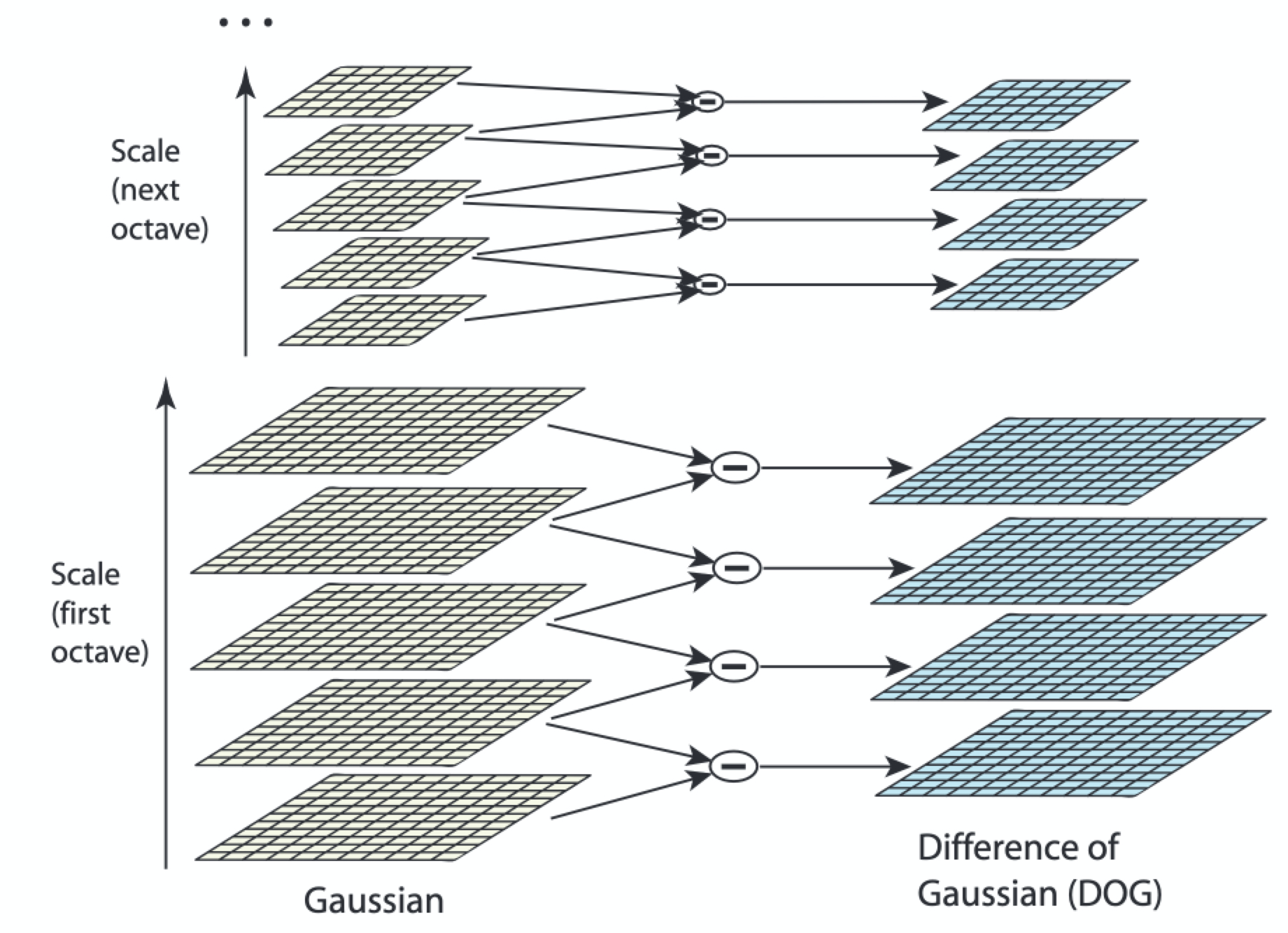
使用高斯金字塔每组中相邻上下两层图像相减，得到高斯差分图像，如图所示，进行极值检测
高斯金字塔有多组，每组又有多层。一组中的多个层之间的尺度是不一样的（也就是使用的高斯参数σσ是不同的），相邻两层之间的尺度相差一个比例因子k
如果每组有S层，则$k = 2^{\frac{1}{S}}$。上一组图像的最底层图像是由下一组中尺度为2σ的图像进行因子为2的降采样得到的（高斯金字塔先从底层建立），当相乘了s次时，将会成为下一次的比例因子2k
高斯金字塔的组数一般是

$o = [\log_2\min(m, n)] - a$,

其中，$o$为高斯金字塔的层数。

$\sigma(o, s) = \sigma_02^{\frac{o + s}{S}}$,

其中，$o$为所在组，$s$为所在的层，$\sigma_0$为初始尺度，$S$为每组的层数。