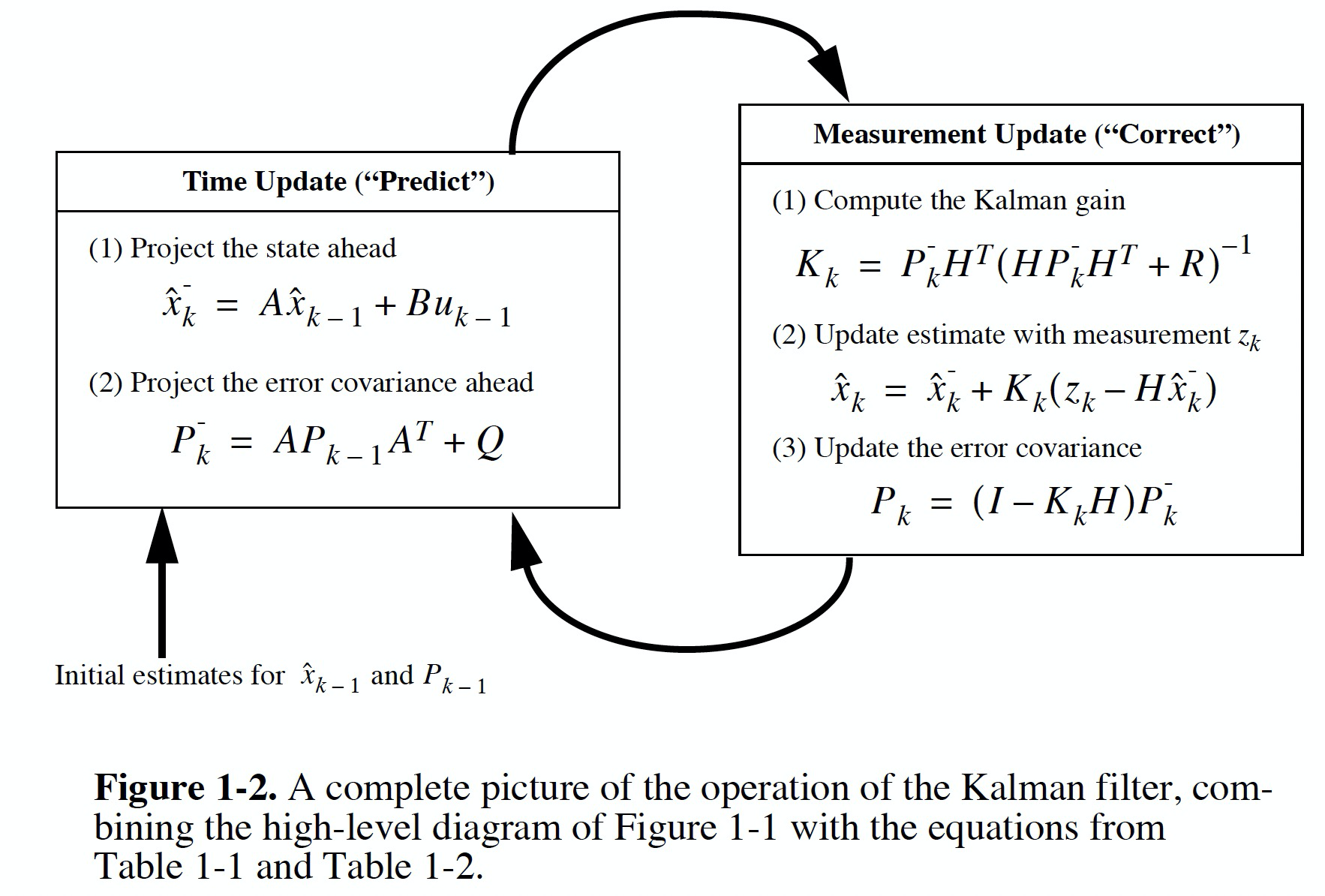
1. 概述
- Welch G, Bishop G. An introduction to the Kalman filter[J]. 1995.
- http://www.cs.unc.edu/~welch/kalman/
2. 基础知识
- 概率
- 概率的本质是用数值表示某件事情发生的可能性
3. 卡尔曼滤波
3.1 运动方程
给定一个线性系统的状态差分方程:
$x_k = Ax_{k-1} + Bu_{k-1} + w_{k-1}$,
其中,$x$是系统的状态向量,大小为$n1$;$A$为状态转移矩阵,大小为$nn$;$u$为系统输入,即控制量,大小为$k1$;$B$是将输入控制量转换为状态量的矩阵,大小为$nk$;$w$为系统噪声,随机变量。
运动方程举例:
一个匀加速运动的小车,受到合理为$f_t$,那么,由$t-1$到$t$时刻的位移和速度计算公式为:
$x_t = x_{t-1} + (\dot{x}_{t-1}*\Delta t) + \frac{f_t(\Delta t)^2}{2m}$,
$\dot{x}_t = \dot{x}_{t-1} + \frac{f_t\Delta t}{m}$.
我们得到:
$x_t = \left[\begin{matrix} x_t \\ \dot{x}_t \end{matrix}\right]$, $u_t = \frac{f_t}{m}$.
$\left[\begin{matrix} x_t \\ \dot{x}_t \end{matrix}\right] = \left[\begin{matrix} 1 & \Delta t \\ 0 & 1 \end{matrix}\right]\left[\begin{matrix} x_{t-1} \\ \dot{x}_{t-1} \end{matrix}\right] + \left[\begin{matrix} \frac{(\Delta t)^2}{2} \\ \Delta t \end{matrix}\right]\frac{f_t}{m}$.
那么,有了该运动方程我们就可以地推得到系统的每一个时刻的状态了。那卡尔曼滤波的作用是什么呢?该运动方程的问题在于在实际中,由于系统的复杂程度,很难建立精确地运动方程。此外,由于运动方程是包含噪声的,即随着时间的推移,状态量的误差会逐步累积,直至误差达到不可用的地步。因此,卡尔曼滤波就发挥作用了。既然,一致利用运动方程地推会产生累计误差,那如果中间有观测数据来校准,就能够减少状态量的误差了。此外,由于观测也不是十分精确的,也会带来噪声,那么如果利用运动方程和观测量来计算系统的精确地状态量,就是卡尔曼滤波发挥作用的地方。
这个观测,或者说是反馈,从概率论贝叶斯模型的观点来看前面预测的结果就是先验,测量出的结果就是后验。
3.2 运动方程的状态量分析
下面先来分析一下状态量及其方差。
目标的状态定义为
$\vec{x} = \left[
\begin{matrix}
p \\
v
\end{matrix}
\right]$,其中$v$表示目标的运动速度,$p$表示目标的当前位置。
卡尔曼滤波假设两个变量(即位置和速度)是随机的,而且符合高斯分布。每个变量都有一个均值$\mu$,它是随机分布的中心;有一个方差$\sigma$,它衡量组合的不确定性。
由于基于旧位置估计新位置,我们会产生这两个结论:如果速度很快,机器人可能移动得更远,所以得到的位置会更远;如果速度很慢,机器人就走不了那么远。这种关系对目标跟踪来说非常重要,因为它提供了更多信息:一个可以衡量可能性的标准。这就是卡尔曼滤波的目标:从不确定信息中挤出尽可能多的信息。为了捕获这种相关性,我们用的是协方差矩阵。简而言之,矩阵的每个值是第i个变量和第j个变量之间的相关程度(由于矩阵是对称的,$i$和$j$的位置可以随便交换)。我们用$\Sigma$表示协方差矩阵,在这个例子中,就是$\Sigma_{ij}$。
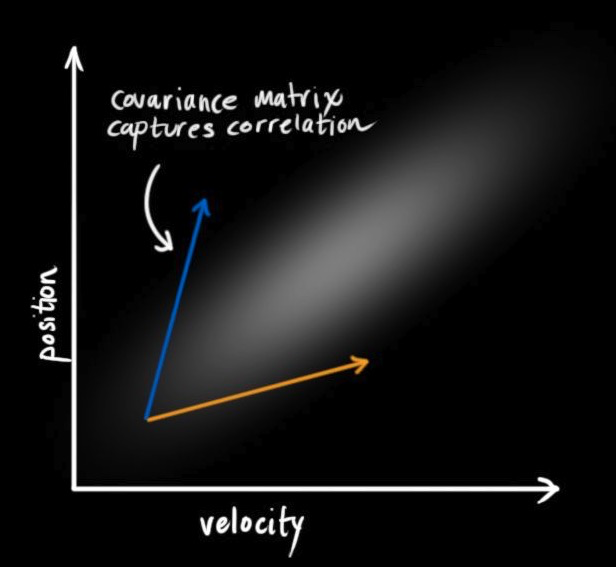
(图片来源:http://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/)
为了把以上关于状态的信息建模为高斯分布(图中色块),我们还需要$k$时的两个信息:最佳估计$\hat{x}$(均值,也就是$\mu$,协方差矩阵$P_k$。(虽然还是用了位置和速度两个变量,但只要和问题相关,卡尔曼滤波可以包含任意数量的变量)。
$\hat{x} = \left[
\begin{matrix}
p \\
v
\end{matrix}
\right]$, $P_{k} = \left[
\begin{matrix}
\Sigma_{pp} & \Sigma_{pv} \\
\Sigma_{vp} & \Sigma_{vv}
\end{matrix}
\right]$.
接下来,我们利用$k-1$时刻的状态来预测$k$时刻的状态。从$k-1$时刻到$k$时刻,状态变换矩阵定义为$F_k$,如下图所示。它从原始预测中取每一点,并将其移动到新的预测位置。如果原始预测是正确的,系统就会移动到新位置。
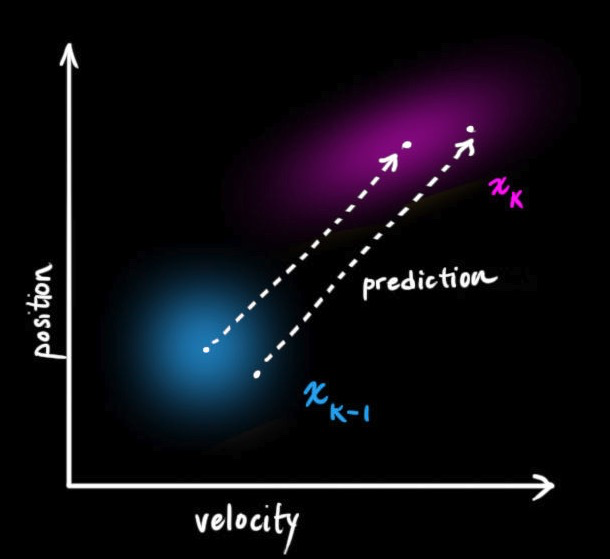
(图片来源:http://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/)
假设目标的运动方程为
$p_k = p_{k-1}+ \Delta tv_{k-1}$,
$v_k = v_{k-1}$,
那么,由$\hat{x}_k = \left[
\begin{matrix}
1 & \Delta t \\
0 & 1
\end{matrix}
\right]\hat{x}_{k-1} = F_k\hat{x}_{k-1}$得,$F_k = \left[
\begin{matrix}
1 & \Delta t \\
0 & 1
\end{matrix}
\right]$。
这是一个预测矩阵,它能给出机器人的下一个状态,但目前我们还不知道协方差矩阵的更新方法。这也是我们要引出下面这个等式的原因:如果我们将分布中的每个点乘以矩阵A,那么它的协方差矩阵为
$Cov(x) = \Sigma$,
$Cov(Ax) = A\Sigma A^T$.
因此,我们得到
$\hat{x}_k = F_k\hat{x}_{k-1}$,
$P_k = F_kP_{k-1}F_k^T$.
其中,$P_k$表示的就是预测值和真实值之间的误差协方差。
接下来,我们推导误差写方程是如何从k-1时刻通过预测方程传递到k时刻的。
假设$\vec{x}_k$为t时刻下状态向量的真值,我们得到,
$\vec{x}_k - \hat{\vec{x}}_{k|k-1} = F(\vec{x}_{k-1} - \hat{\vec{x}}_{k|k-1}) + w_k$,
而$P_{k|k-1} = E[(\vec{x}_k - \hat{\vec{x}}_{k|k-1})(\vec{x}_k - \hat{\vec{x}}_{k|k-1})^T] = E[(F(\vec{x}_k - \hat{\vec{x}}_{k|k-1}) + w_k)(F(\vec{x}_k - \hat{\vec{x}}_{k|k-1}) + w_k))^T]$
$= F(E[(\vec{x}_k - \hat{\vec{x}}_{k|k-1})(\vec{x}_k - \hat{\vec{x}}_{k|k-1})^T])F^T + FE[(\vec{x}_k - \hat{\vec{x}}_{k|k-1})w_k^T]F^T$
$+ FE[(w_k\vec{x}_k - \hat{\vec{x}}_{k|k-1})^T]F^T + E[w_kw_k^T]$.
考虑到状态向量和噪声是不相关的,则$E[(w_t\vec{x}_k - \hat{\vec{x}}_{k|k-1})^T] = 0$,上式可以简化为
$P_{k|k-1} = FE[(\vec{x}_{k-1} - \hat{\vec{x}}_{k|k-1})(\vec{x}_{k-1} - \hat{\vec{x}}_{k|k-1})^T]F^T + E[w_kw_k^T]$
$= F_kP_{k-1}F_k^T + Q_k$
现在,我们考虑加速度计输入,定义为$\vec{u}_k$。那么,运动方程进一步写成
$p_k = p_{k-1} + \Delta t v_{k-1} + \frac{1}{2}a\Delta t$,
$v_k = v_{k-1} + a\Delta t$.
由于预测也是有误差的,否则我们就直接使用预测结果来作为目标的下一步状态。因此,我们需要一个不确定性来衡量预测可能带来的误差。如下图所示,加上预测不确定性后,$\hat{x}_{k-1}$的每个预测状态都可能会移动到另一点,也就是蓝色的高斯分布会移动到紫色高斯分布的位置,并且具有协方差$Q_k$,换句话说,我们把这些不确定影响视为协方差$Q_k$的噪声。这个紫色的高斯分布拥有和原分布相同的均值,但协方差不同。

(图片来源:http://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/)

(图片来源:http://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/)
此处,我们得到的预测方程和协方差方程为
$\hat{x}_k = F_k\hat{x}_{k-1} + B_k\vec{u}_k$,
$P_k = F_kP_{k-1}F_{k}^{T}+Q_k$.
这两个公式主要思想如下:
- 新的估计结果是基于原估计结果和已知外部输入校正后得到的预测结果
- 新的不确定性是基于原不确定性和外部输入的不确定性得到的预测不确定性
3.3 观测方程
基于运动预测方程,当有额外传感器输入观测数据时,我们可利用该观测数据来融合预测数据,易获取目标更加准确地状态。观测是一系列读数,其与状态之间存在一定变换关系,定义为H矩阵。在刚刚的一维情况的小例子中,我们其实做了一个隐式的假设,即有预测更新得到的位置的概率分布和测距仪所得的测量值具有相同的单位 (unit),如米 (m)。但实际情况往往不是这样的,比如,测距仪给出的可能不是距离,而是信号的飞行时间(由仪器至小车的光的传播时间),单位为秒 (s)。这样的话,我们就无法直接如上面一般直接将两个高斯分布相乘了。如下图所示,
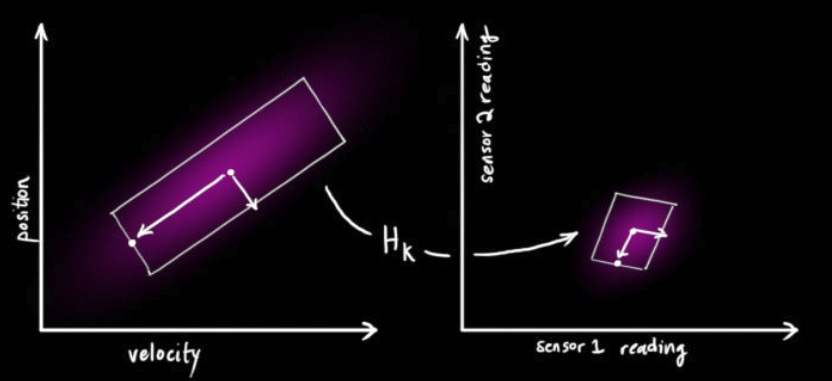
(图片来源:http://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/)
我们得到如下等式,
$\vec{\mu} = H_k\hat{x}_k$,
$\Sigma = H_kP_kH_k^T$.
由于种种因素,传感器记录的信息其实是不准的,一个状态事实上可以产生多种读数。我们将这种不确定性(即传感器噪声)的协方差设为$R_k$,读数的分布均值为$z_k$,如下图所示,

此时,得到了两块高斯分布,一块围绕预测的均值,另一块围绕传感器读数。如下图所示,
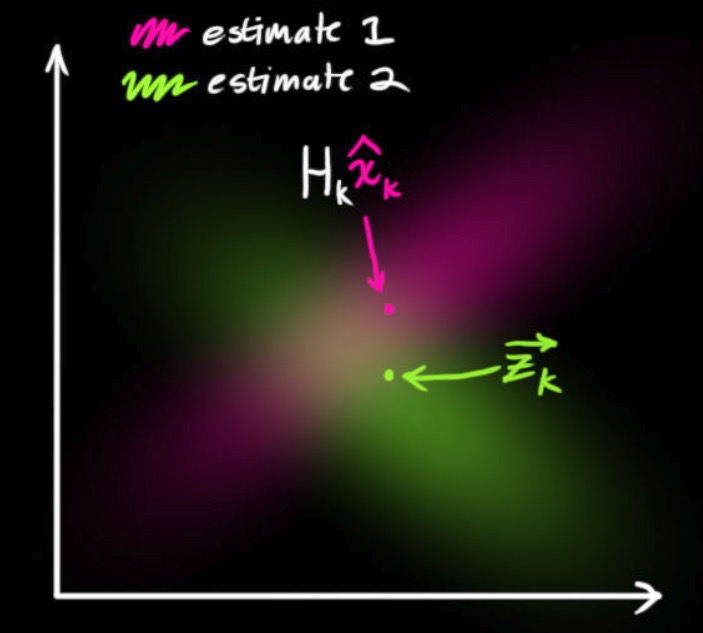
(图片来源:http://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/)
3.4 基于高斯分布的预测和观测融合
如果要生成靠谱预测,模型必须调和这两个信息。也就是说,对于任何可能的读数$z_1, z_2$,这两种方法预测的状态都有可能是准的,也都有可能是不准的。重点是我们怎么找到这两个准确率。最简单的方法是两者相乘,可以得到它们的重叠部分,这也是会出现最佳估计的区域。换个角度看,它看起来也符合高斯分布。当你把两个高斯分布和它们各自的均值和协方差矩阵相乘时,你会得到一个拥有独立均值和协方差矩阵的新高斯分布。最后剩下的问题就不难解决了:我们必须有一个公式来从旧的参数中获取这些新参数!
下面将要讨论两个一维高斯分布得到更加准确地高斯分布。
设方差为$\sigma^2$,均值为$\mu$,高斯分布一般形式为$N(x, \mu, \sigma) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$,那么两条高斯曲线相乘后的曲线大约如下图所示,
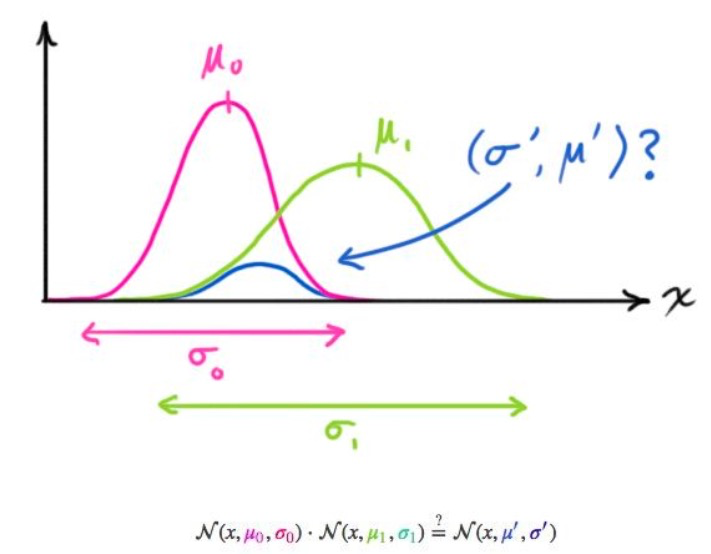
(图片来源:http://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/)
把这个式子按照一维方程进行扩展,可得:
$\mu’ = \mu_0 + \frac{\sigma_0^2(\mu_1 - \mu_0)}{\sigma_0^2 + \sigma_1^2}$,
$\sigma’^2 = \sigma_0^2 - \frac{\sigma_0^4}{\sigma_0^2 + \sigma_1^2}$.
如果有些太复杂,我们用k简化一下,
$k = \frac{\sigma_0^2}{\sigma_0^2 + \sigma_1^2}$,
$\mu’ = \mu_0 + k(\mu_1 - \mu_0)$,
$\sigma’^2 = \sigma_0^2 - k\sigma_0^2$.
以上是一维的内容,如果是多维空间,把这个式子转成矩阵格式:
$K = \Sigma_0(\Sigma_0 + \Sigma_1)^{-1}$,
$\vec{\mu}’ = \vec{\mu}_0 + K(\vec{\mu}_1 - \vec{\mu}_0)$,
$\Sigma’ = \Sigma_0 - K\Sigma_0$.
这个矩阵K就是卡尔曼增益。
基于以上基础,我们开始推导卡尔曼滤波的更新过程。
截至目前,我们有用矩阵$(\mu_0, \Sigma_0) = (H_k\hat{x}_k, H_kP_kH_k^T)$预测的分布,有用传感器读数$(\mu_1, \Sigma_1) = (\vec{z}_k, R_k)$预测的分布。把它们代入上节的矩阵等式中:
$H_k\hat{x}_k’ = H_k\hat{x}_k + K(\vec{z}_k - H_k\hat{x}_k)$,
$H_kP_k’H_k^T = H_kP_kH_k^T - KH_kP_kH_k^T$.
卡尔曼增益就是:
$K = H_kP_kH_k^T(H_kP_kH_k^T + R_k)^{-1}$.
考虑到$K$里还包含着一个$H_k$,再精简一下上式:
$\hat{x}_k’ = \hat{x}_k + K’(\vec{z}_k - H_k\hat{x}_k)$,
$P_k’ = P_k - K’H_kP_k$,
$K’ = P_kH_k^T(H_kP_kH_k^T + R_k)^{-1}$.
$\hat{x}_k’$是最佳估计值,我们可以把它继续放进去做另一轮预测。
3.5 总结
卡尔曼滤波的流程可总结为下图: