1. 高斯模糊概述

高斯模糊(英语: Gaussian Blur), 也叫高斯平滑, 是在 Adobe Photoshop, GIMP 以及 Paint.NET 等图像处理软件中广泛使用的处理效果, 通常用它来减少图像噪声以及降低细节层次.

从数学的角度来看, 图像的高斯模糊过程就是图像与正态分布做卷积. 由于正态分布又叫作高斯分布, 所以这项技术就叫作高斯模糊.
由于高斯函数的傅立叶变换是另外一个高斯函数, 所以高斯模糊对于图像来说就是一个低通滤波器.

2. 原理

所谓”模糊”，可以理解成每一个像素都取周边像素的平均值，如下图所示：

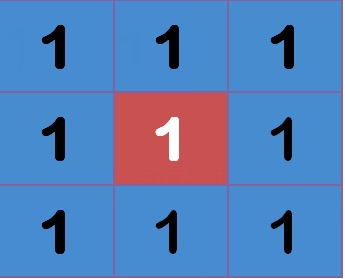
“中间点”取”周围点”的平均值，就是1。在数值上，这是一种”平滑化”。

在图形上，就相当于产生”模糊”效果，”中间点”失去细节。显然，计算平均值时，取值范围越大，”模糊效果”越强烈。
从数值角度看，就是数值越平滑。

接下来的问题就是，既然每个点都要取周边像素的平均值，那么应该如何分配权重呢？如果使用简单平均，显然不是很合理，因为图像都是连续的，越靠近的点关系越密切，越远离的点关系越疏远。因此，加权平均更合理，距离越近的点权重越大，距离越远的点权重越小。

2.1 正态分布的权重

正态分布显然是一种可取的权重分配模式。在图形上，正态分布是一种钟形曲线，越接近中心，取值越大，越远离中心，取值越小。计算平均值的时候，我们只需要将”中心点”作为原点，其他点按照其在正态曲线上的位置，分配权重，就可以得到一个加权平均值。

一维高斯函数如下公式所述：

$G(x) = \frac{1}{2\pi \sigma^{2}}e^{-\frac{x^2}{2\sigma^2}}$ ，

其中，由于对于中心点而言，$\mu = 0$。

图像是二维的，因此，图像对应的高斯函数如下公式所述：

$G(x, y, \sigma) = \frac{1}{2\pi \sigma^{2}}e^{-\frac{x^2 + y^2}{2\sigma^2}}$ .

有了这个函数，就可以计算每个点的权重了。

2.2 $\sigma$值介绍

尺度参数$\sigma$决定了分布幅度，在高斯模糊处理中，$\sigma$常取 1.5。

2.3 权重矩阵计算

假定中心点的坐标是（0,0），那么距离它最近的8个点的坐标如下：

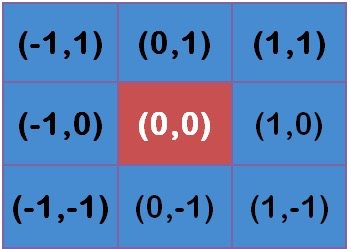
为了计算权重矩阵，需要设定$\sigma$的值。假定$\sigma = 1.5$，则模糊半径为1的权重矩阵如下：

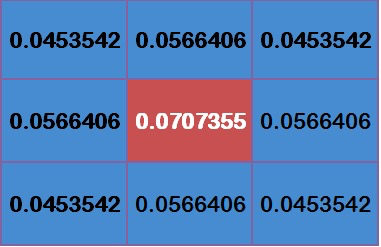
这9个点的权重总和等于0.4787147，如果只计算这9个点的加权平均，还必须让它们的权重之和等于1，因此上面9个值还要分别除以0.4787147，得到最终的权重矩阵。

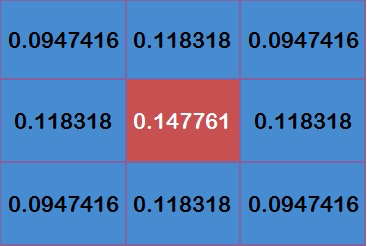
2.4 计算高斯模糊

假设现有9个像素点，灰度值（0-255）如下：

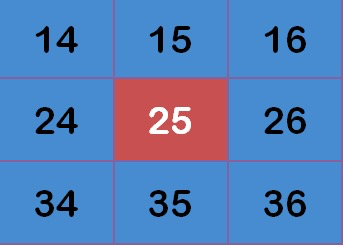
每个点乘以自己的权重值：

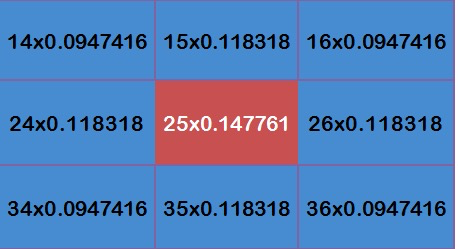
得到：

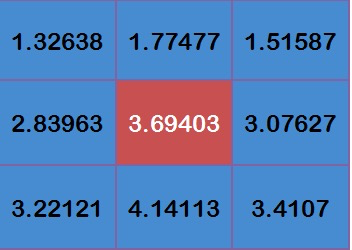
将这9个值加起来，就是中心点的高斯模糊的值。

对所有点重复这个过程，就得到了高斯模糊后的图像。如果原图是彩色图片，可以对RGB三个通道分别做高斯模糊。

2.5 边界点的处理

一个变通方法，就是把已有的点拷贝到另一面的对应位置，模拟出完整的矩阵。
填充0。

3. 代码实现

import math

import numpy as np
import PIL.Image
import PIL.ImageFilter
import scipy.misc
import scipy.signal

# 概率密度函数
def get_cv(r, sigma):
    return 1 / (2 * math.pi * sigma ** 2) * math.exp((-r**2) / (2 * sigma ** 2))

# 高斯滤波掩模
def get_window():
    # 模糊半径为 2, sigma 为 1.5
    radius, sigma = 2, 1.5
    window = np.zeros((radius * 2 + 1, radius * 2 + 1))
    for i in range(-radius, radius + 1):
        for j in range(-radius, radius + 1):
            r = (i ** 2 + j ** 2) ** 0.5
            window[i + radius][j + radius] = get_cv(r, sigma)
    return window / np.sum(window)


def convert_2d(r):
    window = get_window()
    s = scipy.signal.convolve2d(r, window, mode='same', boundary='symm')
    return s.astype(np.uint8)


def convert_3d(r):
    s_dsplit = []
    for d in range(r.shape[2]):
        rr = r[:, :, d]
        ss = convert_2d(rr)
        s_dsplit.append(ss)
    s = np.dstack(s_dsplit)
    return s


im = PIL.Image.open('/img/jp.jpg')
im_mat = scipy.misc.fromimage(im)
im_converted_mat = convert_3d(im_mat)
im_converted = PIL.Image.fromarray(im_converted_mat)
im_converted.show()

vSLAMNet（三）-数字图像处理-高斯滤波