1. 概述
- Madgwick S. An efficient orientation filter for inertial and inertial/magnetic sensor arrays[J]. Report x-io and University of Bristol (UK), 2010, 25: 113-118.
- Madgwick S O H, Harrison A J L, Vaidyanathan R. Estimation of IMU and MARG orientation using a gradient descent algorithm[C]//2011 IEEE international conference on rehabilitation robotics. IEEE, 2011: 1-7.
- 位姿估计
- 传感器
- 陀螺仪 + 加速度计
- 陀螺仪 + 加速度计 + 磁力计
- 优点
- 计算量低,适用于轻量级设备
- 适用于低采样频率
- 仅有2个需要调的参数
- 核心思想
- 首先,通过陀螺仪的角速度初步计算传感器方向偏移$^{E}_{S}q_{w,t}$;然后,通过对重力加速度和地磁这两个恒定量在传感器坐标系下的投影计算传感器方向偏移$^{E}_{S}q_{\nabla,t}$;最后通过互补滤波器融合$^{E}_{S}q_{w,t}$和$^{E}_{S}q_{\nabla,t}$来得到一个更加可信的结果。除此之外还需要校正地磁计数据畸变和陀螺仪零点漂移。
2. 算法详解
2.1 陀螺仪姿态解算
主要思想
- 建立四元数和陀螺仪读数之间的微分方程
- 欧拉中值积分
坐标系定义
- 世界坐标系E
- 传感器坐标系S
- $^{S}_{E}q$表示坐标系E相对于坐标系S的单位旋转四元数
- 陀螺仪数据输出
- $^{S}w = [0 w_x w_y w_z]$
- 地面参考系(Earth)相对于传感器参考系(Sensor)的旋转可以由其四元数的导数对时间的积分获得,$^{S}_{E}q_{w,t} = ^{S}_{E}\hat{q}_{est.t-1} + ^{S}_{E}q_{w,t}\Delta t$,其中$^{S}_{E}\dot{q} = \frac{1}{2}^{S}_{E}\hat{q} \otimes ^{S}w$,$^{S}_{E}\dot{q}$表示姿态四元数变化的速度。该公式中的角速度可以直接从传感器读出,上一时刻的位姿也是已知,时间间隔也可以从传感器芯片中的获得。可以轻松的计算出结果,下面推导下该公式
已知t时刻的四元数$^{S}_{E}q_{t-1}$和角速度$^{S}w_{t-1}$、t时刻的加速度$^{S}w_t$,系统采样间隔为$\Delta t$,求t时刻的四元数$^{S}_{E}q_{t}$。
基于常微分方程,套用中值积分公式,得到$^{S}_{E}q_t = ^{S}_{E}q_{t-1} + \frac{\Delta t}{2}(K_1 + K_2)$,其中,$K_1 = \frac{1}{2}^{S}_{E}q_{t-1}\otimes ^{S}w_{t-1}$和$K_2 = \frac{1}{2}(^{S}_{E}q_{t-1} + \Delta tK_1)\otimes^{S}w_t$。
此处,近似估计物体四元数在t-1到t时刻之间的平均变化速度$^{S}_{E}\dot{q}_{w,t-1,t}$。在实际过程中,往往并不能得到t-1时刻的准确的四元数,二是一个最优的估计值$^{S}_{E}\hat{q}_{est,t-1}$。
我们得到$^{S}_{E}\dot{q}_{w,t-1,t} = \frac{1}{2}(K_1 + K_2) = \frac{1}{2}(\frac{1}{2}^{S}_{E}\hat{q}_{est,t-1}\otimes ^{S}w_{t-1} + \frac{1}{2}(^{S}_{E}\hat{q}_{est,t-1} + \Delta t(\frac{1}{2}^{S}_{E}\hat{q}_{est,t-1}\otimes ^{S}w_{t-1})) \otimes ^{S}w_{t})$
$^{S}_{E}q_{w,t} = ^{S}_{E}\hat{q}_{est,t-1} + ^{S}_{E}\dot{q}_{w,t-1,t}\Delta t$
从而得到,
$^{S}_{E}q_{w,t} = ^{S}_{E}\hat{q}_{est,t-1} + \frac{\Delta}{2}(\frac{1}{2}^{S}_{E}\hat{q}_{est,t-1}\otimes ^{S}w_{t-1} + \frac{1}{2}(^{S}_{E}\hat{q}_{est,t-1} + \Delta t(\frac{1}{2}^{S}_{E}\hat{q}_{est,t-1}\otimes ^{S}w_{t-1})) \otimes ^{S}w_{t})$
以上迭代公式是计算精度要求较高时采用的。而在实际工程中,不要求如此的高精度而追求计算速度时,可采用以下的近似迭代公式。亦是参考Madgwick算法详细解读。
在t-1时刻到t时刻之间的变化速度$^S_E\dot{q}_{w,t-1,t}$可近似为,
$^S_E\dot{q}_{w,t-1,t} = \frac{1}{2}^S_E\hat{q}_{est,t-1}\otimes ^Sw_t$,
所以,$^S_Eq_{w,t} = ^S_E\hat{q}_{est,t-1} + ^S_E\dot{q}_{w,t-1,t}\Delta t = ^S_E\hat{q}_{est,t-1} + (\frac{1}{2}^S_E\hat{q}_{est,t-1}\otimes ^Sw_t)\Delta t$.
2.2 加速度计和磁力计姿态解算
- 传感器介绍
- 加速度计
- 测量重力和外界施加给物体的力产生的加速度的和
- 磁力计
- 测量地球磁场和外界地磁干扰在传感器坐标系下的磁通量
- 加速度计
- 假设
- 该算法假设加速度计和磁力计分别仅仅观测重力和地球磁场
- 目标
- 利用加速度计和磁力计求解姿态$^{S}_{E}q_{\bigtriangledown, t}$
以上的推导参考Madgwick算法详细解读,推导思路同论文一致,只是有些符号定义不同。此外,论文中首先分别对加速度计读数和磁力计读数进行推导,然后组合在一起。以下的推导直接将加速度计读数和磁力计读数组合在一起。
当物体静止朝北时,加速度计理论输出为$^{E}\hat{g} = [0\ 0\ 0\ 1]$,磁力计理论输出为$^E\hat{b} = [0\ b_x\ 0\ b_z]$,表示为实部为0的四元数。进一步地,我们得到向量$^E\hat{y} = [0\ 0\ 1\ b_x\ 0\ b_z]$。
当物体运动后,在t时刻,我们得到新的加速度计和磁力计的向量分别为$^S\hat{a}_t = [0\ a_x\ a_y\ a_z]$和$^S\hat{m}_t = [0\ m_x\ m_y\ m_z]$。进一步地,我们得到新的向量$^S\hat{y}_t = [a_x\ a_y\ a_z\ m_x\ m_y\ m_z]$。
设t时刻物体的姿态为$^{S}_{E}q_t$,那么根据四元数旋转可得到,
$^S\hat{a}_t = ^{S}_{E}q_t \otimes ^E\hat{g} \otimes ^{S}_{E}q_t^*$,
$^S\hat{m}_t = ^{S}_{E}q_t \otimes ^E\hat{b} \otimes ^{S}_{E}q_t^*$。
利用旋转矩阵表示为,
$^S\hat{a}_t^T = R_t ^E\hat{g}^T$,
$^S\hat{m}_t^T = R_t ^E\hat{b}^T$,
将$R_t$组合为新的矩阵$M_t$,
$M_t = \left[
\begin{matrix}
R_t & 0 \\
0 & R_t
\end{matrix}
\right]$,
那么,我们得到,
$^S\hat{y}_t^T = M_t^E\hat{y}^T$.
上式中,$^S\hat{y}_t$和$^E\hat{y}$是已知的,可以求出$^{S}_{E}q_t$,即估计值$^{S}_{E}\hat{q}_t = [q_0\ q_1\ q_2\ q_3]^T$,由此转换成$\hat{M}_t$,使得误差平方和$F(^{S}_{E}\hat{q}_t, ^E\hat{y}, ^S\hat{y}_t)$最小,得到如下优化方程,
$\min_{^{S}_{E}\hat{q}_t\in R^4}F(^{S}_{E}\hat{q}_t, ^E\hat{y}, ^S\hat{y}_t)$,
其中,$F(^{S}_{E}\hat{q}_t, ^E\hat{y}, ^S\hat{y}_t) = ||f(^{S}_{E}\hat{q}_t, ^E\hat{y}, ^S\hat{y}_t)||^2 = (\hat{M}_t\ ^E\hat{y}^T - ^S\hat{y}_t^T)^T(\hat{M}_t\ ^E\hat{y}^T - ^S\hat{y}_t^T)$。
函数$f(\cdot)$回一个多元向量函数,采用数值解法,例如梯度下降法、牛顿法等。论文中采用梯度下降法。
设$^{S}_{E}\hat{q}_t$的初值为$^{S}_{E}\hat{q}_{t,k}$,为4行1列矩阵,那么误差平方和为$F(^{S}_{E}\hat{q}_{t,k}, ^E\hat{y}, ^S\hat{y}_t$。假设初值四元数需要修正的量为$\bigtriangledown f(^{S}_{E}\hat{q}_{t,k}, ^E\hat{y}, ^S\hat{y}_t)$,那么修正后的误差平方和为$F(^{S}_{E}\hat{q}_{t,k} + \bigtriangledown f, ^E\hat{y}, ^S\hat{y}_t)$。
由泰勒公式展开得到,
$F(^{S}_{E}\hat{q}_{t,k} + \bigtriangledown f, ^E\hat{y}, ^S\hat{y}_t) = F(^{S}_{E}\hat{q}_{t,k}, ^E\hat{y}, ^S\hat{y}_t) + \frac{\partial F(^{S}_{E}\hat{q}_{t,k}, ^E\hat{y}, ^S\hat{y}_t)}{\partial q}\bigtriangledown f + O(||\bigtriangledown f||^2) \approx F(^{S}_{E}\hat{q}_{t,k}, ^E\hat{y}, ^S\hat{y}_t) + \frac{\partial F(^{S}_{E}\hat{q}_{t,k}, ^E\hat{y}, ^S\hat{y}_t)}{\partial q}\bigtriangledown f$,
其中,$\bigtriangledown f$为4行1列矩阵,$\frac{\partial F(^{S}_{E}\hat{q}_{t,k}, ^E\hat{y}, ^S\hat{y}_t)}{\partial q}$为1行4列矩阵,得到,
$\frac{\partial F(^{S}_{E}\hat{q}_{t,k}, ^E\hat{y}, ^S\hat{y}_t)}{\partial q} = [\frac{\partial F}{\partial q_0}\ \frac{\partial F}{\partial q_1}\ \frac{\partial F}{\partial q_2}\ \frac{\partial F}{\partial q_3}]$,
那么,梯度为,
$\lim_{\bigtriangledown f\rightarrow 0}\frac{F(^{S}_{E}\hat{q}_{t,k} + \bigtriangledown f, ^E\hat{y}, ^S\hat{y}_t) - F(^{S}_{E}\hat{q}_{t,k}, ^E\hat{y}, ^S\hat{y}_t)}{||\bigtriangledown f||} = \frac{\partial F(^{S}_{E}\hat{q}_{t,k}, ^E\hat{y}, ^S\hat{y}_t)}{\partial q}\frac{\bigtriangledown f}{||\bigtriangledown f||} = ||\frac{\partial F(^{S}_{E}\hat{q}_{t,k}, ^E\hat{y}, ^S\hat{y}_t)}{\partial q}||\cos \theta$,
其中,$\theta$为向量$(\frac{\partial F(^{S}_{E}\hat{q}_{t,k}, ^E\hat{y}, ^S\hat{y}_t)}{\partial q})^T$与单位向量$\frac{\bigtriangledown f}{||\bigtriangledown f||}$的夹角。当$\theta = \pi$时,误差平方和下降最快。因此,我们得到,
$\bigtriangledown f = -\rho (\frac{\partial F(^{S}_{E}\hat{q}_{t,k}, ^E\hat{y}, ^S\hat{y}_t)}{\partial q})^T$,
其中,$\rho$为一个大于0的比例系数。上式中的$F(^{S}_{E}\hat{q}_{t,k}, ^E\hat{y}, ^S\hat{y}_t)$关于四元数q的偏导计算为,
$\frac{\partial F(^{S}_{E}\hat{q}_{t,k}, ^E\hat{y}, ^S\hat{y}_t)}{\partial q} = \frac{\partial (f^T(^{S}_{E}\hat{q}_t, ^E\hat{y}, ^S\hat{y}_t)f(^{S}_{E}\hat{q}_t, ^E\hat{y}, ^S\hat{y}_t))}{\partial q}$
$= [\frac{\partial (f_{11}^2 + f_{21}^2 + \cdots + f_{61}^2)}{\partial q_0}\ \frac{\partial (f_{11}^2 + f_{21}^2 + \cdots + f_{61}^2)}{\partial q_1}\ \frac{\partial (f_{11}^2 + f_{21}^2 + \cdots + f_{61}^2)}{\partial q_2}\ \frac{\partial (f_{11}^2 + f_{21}^2 + \cdots + f_{61}^2)}{\partial q_3}]$
$= [2f_{11}\frac{\partial f_{11}}{\partial q_0} + \cdots + 2f_{61}\frac{\partial f_{61}}{\partial q_0}\ 2f_{11}\frac{\partial f_{11}}{\partial q_1} + \cdots + 2f_{61}\frac{\partial f_{61}}{\partial q_1}\ 2f_{11}\frac{\partial f_{11}}{\partial q_2} + \cdots + 2f_{61}\frac{\partial f_{61}}{\partial q_2}\ 2f_{11}\frac{\partial f_{11}}{\partial q_3} + \cdots + 2f_{61}\frac{\partial f_{61}}{\partial q_3}]$
$= 2f^T(^{S}_{E}\hat{q}_t, ^E\hat{y}, ^S\hat{y}_t)\frac{\partial f(^{S}_{E}\hat{q}_t, ^E\hat{y}, ^S\hat{y}_t)}{\partial q}$,
其中,$f_{ij}$表示$f(^{S}_{E}\hat{q}_t, ^E\hat{y}, ^S\hat{y}_t)$中第i行第j列元素。$f(^{S}_{E}\hat{q}_t, ^E\hat{y}, ^S\hat{y}_t)$的表达式为,
$f(^{S}_{E}\hat{q}_t, ^E\hat{y}, ^S\hat{y}_t) = \hat{M}_t\ ^E\hat{y}^T - ^S\hat{y}_t^T$
$= \left[
\begin{matrix}
2(q_1q_3 - q_0q_2) - a_x \\
2(q_0q_1 + q_2q_3) - a_y \\
2(\frac{1}{2} - q_1^2 - q_2^2) \\
2b_x(\frac{1}{2} - q_2^2 - q_3^2) + 2b_z(q_1q_3 - q_0q_2) - m_x \\
2b_x(q_1q_2 - q_0q_3) + 2b_z(q_0q_1 + q_1q_3) - m_y \\
2b_x(q_0q_2 + q_1q_3) + 2b_z(\frac{1}{2} - q_1^2 - q_2^2) - m_z
\end{matrix}
\right]$.
而$\frac{\partial f(^{S}_{E}\hat{q}_{t,k}, ^E\hat{y}, ^S\hat{y}_t)}{\partial q}$是$f(^{S}_{E}\hat{q}_{t,k}, ^E\hat{y}, ^S\hat{y}_t)$关于四元数的偏导,其雅可比矩阵为,
$\frac{\partial F(^{S}_{E}\hat{q}_{t,k}, ^E\hat{y}, ^S\hat{y}_t)}{\partial q} = J(^{S}_{E}\hat{q}_{t,k}, ^E\hat{y}, ^S\hat{y}_t))$
$ = [\frac{\partial f(^{S}_{E}\hat{q}_{t,k}, ^E\hat{y}, ^S\hat{y}_t)}{\partial q_0}\ \frac{\partial f(^{S}_{E}\hat{q}_{t,k}, ^E\hat{y}, ^S\hat{y}_t)}{\partial q_1}\ \frac{\partial f(^{S}_{E}\hat{q}_{t,k}, ^E\hat{y}, ^S\hat{y}_t)}{\partial q_2}\ \frac{\partial f(^{S}_{E}\hat{q}_{t,k}, ^E\hat{y}, ^S\hat{y}_t)}{\partial q_3}]$
$= \left[
\begin{matrix}
-2q_2 & 2q_3 & -2q_0 & 2q_1 \\
2q_1 & 2q_0 & 2q_3 & 2q_2 \\
0 & -4q_1 & -4q_2 & 0 \\
-2b_zq_2 & 2b_zq_3 & -4b_xq_2 - 2b_zq_0 & -4b_xq_3 + 2b_zq_1 \\
-2b_xq_3 + 2b_zq_1 & 2b_xq_2 + 2b_zq_0 & 2b_xq_1 + 2b_zq_3 & -2b_xq_0 + 2b_zq_2 \\
2b_xq_2 & 2b_xq_3 - 4b_zq_1 & 2b_xq_0 - 4b_zq_2 & 2b_xq_1
\end{matrix}
\right]$,
因此,$\bigtriangledown f$的计算为,
$\bigtriangledown f(^{S}_{E}\hat{q}_t, ^E\hat{y}, ^S\hat{y}_t) = -rho(2f^T(^{S}_{E}\hat{q}_t, ^E\hat{y}, ^S\hat{y}_t)J(^{S}_{E}\hat{q}_t, ^E\hat{y}, ^S\hat{y}_t))^T$
$= -2\rho J^T(^{S}_{E}\hat{q}_t, ^E\hat{y}, ^S\hat{y}_t)f(^{S}_{E}\hat{q}_t, ^E\hat{y}, ^S\hat{y}_t)$.
进行归一化,除以其范数,得到梯度方向为,
$\frac{\bigtriangledown f(^{S}_{E}\hat{q}_t, ^E\hat{y}, ^S\hat{y}_t)}{||\bigtriangledown f(^{S}_{E}\hat{q}_t, ^E\hat{y}, ^S\hat{y}_t)||} = \frac{-2\rho J^T(^{S}_{E}\hat{q}_t, ^E\hat{y}, ^S\hat{y}_t)f(^{S}_{E}\hat{q}_t, ^E\hat{y}, ^S\hat{y}_t)}{||-2\rho J^T(^{S}_{E}\hat{q}_t, ^E\hat{y}, ^S\hat{y}_t)f(^{S}_{E}\hat{q}_t, ^E\hat{y}, ^S\hat{y}_t)||}$
$= \frac{-J^T(^{S}_{E}\hat{q}_t, ^E\hat{y}, ^S\hat{y}_t)f(^{S}_{E}\hat{q}_t, ^E\hat{y}, ^S\hat{y}_t)}{||-J^T(^{S}_{E}\hat{q}_t, ^E\hat{y}, ^S\hat{y}_t)f(^{S}_{E}\hat{q}_t, ^E\hat{y}, ^S\hat{y}_t)||}$,
然后再乘以步长$\mu_t$就得到各个变量要改变的值。因此,各个自变量现有的值加上要修正的量,得到新的$^S_E\hat{q}_t$的估计为,
$^S_E\hat{q}_{t,k} = ^S_E\hat{q}_{t,k-1} + \frac{\bigtriangledown f(^{S}_{E}\hat{q}_t, ^E\hat{y}, ^S\hat{y}_t)}{||\bigtriangledown f(^{S}_{E}\hat{q}_t, ^E\hat{y}, ^S\hat{y}_t)||}\mu_t$,
其中,$k = 1, 2, \cdots, n$.
如此迭代下去,用上一时刻的姿态$^S_E\hat{q}_{est,t-1}$作为初值$^S_E\hat{q}_{t,0}$,即已知上一次的估计$^S_E\hat{q}_{t,k}$,代入上述公式中,进行多次迭代,直到$F(^{S}_{E}\hat{q}_{t,k}, ^E\hat{y}, ^S\hat{y}_t)$小于某一阈值,或者经过多次迭代,直到满足$F(^{S}_{E}\hat{q}_{t,k}, ^E\hat{y}, ^S\hat{y}_t) - F(^{S}_{E}\hat{q}_{t,k-1}, ^E\hat{y}, ^S\hat{y}_t) \geq 0$,此时,$^S_E\hat{q}_{t,k}$为$^S_E\hat{q}_{t}$的最佳估计值。
以上迭代公式是计算精度要求较高时采用的。而在实际工程中,不要求如此的高精度而追求计算速度时,可采用以下的近似迭代公式。亦是参考Madgwick算法详细解读。
梯度下降法的迭代过程,也可以只用一步来简化,即认为一步就可以近似达到最佳估计值。那就是要设置步长$\mu_t$,使得迭代一次就能够接近最佳估计值,
$\mu_t = \eta||^S_E\dot{q}_{w,t-1,t}||\Delta t$,其中,$\eta \geq 1$,是一个根据实际情况调节的量,用来弥补加速度计和磁力计的测量误差。
因此,简化后的$^S_Eq_{\bigtriangledown, t}$为,
$^S_Eq_{\bigtriangledown, t} = ^S_E\hat{q}_{est,t-1} - \mu_t\frac{\bigtriangledown f(^{S}_{E}\hat{q}_{est,t-1}, ^E\hat{y}, ^S\hat{y}_t)}{||\bigtriangledown f(^{S}_{E}\hat{q}_{est,t-1}, ^E\hat{y}, ^S\hat{y}_t)||}$
$= ^S_E\hat{q}_{est,t-1} - (\eta||^S_E\dot{q}_{w,t-1,t}||\Delta t)\frac{\bigtriangledown f(^{S}_{E}\hat{q}_{est,t-1}, ^E\hat{y}, ^S\hat{y}_t)}{||\bigtriangledown f(^{S}_{E}\hat{q}_{est,t-1}, ^E\hat{y}, ^S\hat{y}_t)||}$
$^S_E\hat{q}_{est,t-1} - (\eta||\frac{1}{2}^S_E\hat{q}_{est,t-1}\otimes ^Sw_t||\Delta t)\frac{\bigtriangledown f(^{S}_{E}\hat{q}_{est,t-1}, ^E\hat{y}, ^S\hat{y}_t)}{||\bigtriangledown f(^{S}_{E}\hat{q}_{est,t-1}, ^E\hat{y}, ^S\hat{y}_t)||}$
2.3 加权融合
互补滤波的方法将两个部分的加权平均,
$^S_Eq_{est,t} = \alpha_1\ ^S_Eq_{w,t} + \alpha_2\ ^S_Eq_{\bigtriangledown,t}$,
其中,$\alpha_1 + \alpha_2 = 1$,$0 \leq \alpha_1 \leq 1$,$0 \leq \alpha_2 \leq 1$。$\alpha_1$和$\alpha_2$是加权系数,它们是由各自的误差占总体误差的比重所决定的,误差所占的比重越小则加权系数越大。
设采样间隔为$\Delta t$,陀螺仪的单位误差$\beta$可以通过查手册得到,那么陀螺仪的误差为$\beta \Delta t$。而加速度计磁场计共同算出的姿态的误差是由计算方法决定的,计算方法如梯度下降法、高斯牛顿迭代法、牛顿法、共轭梯度法等,由于采用的方法是梯度下降法,所以其误差为梯度下降法中所选取的步长$\mu_t$,步长越长则其计算结果的误差越大。所以,总体误差为$\beta \Delta t + \mu_t$。
$\alpha_1$是陀螺仪的姿态加权系数,$\alpha_1 = 1 - \frac{\beta \Delta t}{\beta \Delta t + \mu_t}$。
$\alpha_2$是加速度计和磁力计的姿态加权系数,$\alpha_2 = \alpha_1 = 1 - \frac{\mu_t}{\beta \Delta t + \mu_t}$。
所以,
$^S_Eq_{est,t} = \alpha_1\ ^S_Eq_{w,t} + \alpha_2\ ^S_Eq_{\bigtriangledown,t}$
$= (1-\frac{\beta\Delta t}{\beta\Delta t + \mu_t})(^S_E\hat{q}_{est,t-1} + ^S_E\dot{q}_{w,t-1,t}\Delta t) + (1-\frac{\mu_t}{\beta\Delta t + \mu_t})(^S_E\hat{q}_{est,t-1} - \mu_t\frac{\bigtriangledown f(^{S}_{E}\hat{q}_{est,t-1}, ^E\hat{y}, ^S\hat{y}_t)}{||\bigtriangledown f(^{S}_{E}\hat{q}_{est,t-1}, ^E\hat{y}, ^S\hat{y}_t)||})$
$= ^S_E\hat{q}_{est,t-1} + \frac{\mu_t}{\beta\Delta t + \mu_t}^S_E\dot{q}_{w,t-1,t}\Delta t - \frac{\beta\Delta t}{\beta\Delta t + \mu_t}\mu_t\frac{\bigtriangledown f(^{S}_{E}\hat{q}_{est,t-1}, ^E\hat{y}, ^S\hat{y}_t)}{||\bigtriangledown f(^{S}_{E}\hat{q}_{est,t-1}, ^E\hat{y}, ^S\hat{y}_t)||}$
$= ^S_E\hat{q}_{est,t-1} + \frac{\eta||^S_E\dot{q}_{w,t-1,t}||\Delta t}{\beta\Delta t + \eta||^S_E\dot{q}_{w,t-1,t}||\Delta t}^S_E\dot{q}_{w,t-1,t}\Delta t - \frac{\beta\Delta t}{\beta\Delta t + \eta||^S_E\dot{q}_{w,t-1,t}||}\eta||^S_E\dot{q}_{w,t-1,t}||\Delta t\frac{\bigtriangledown f(^{S}_{E}\hat{q}_{est,t-1}, ^E\hat{y}, ^S\hat{y}_t)}{||\bigtriangledown f(^{S}_{E}\hat{q}_{est,t-1}, ^E\hat{y}, ^S\hat{y}_t)||}$
$= ^S_E\hat{q}_{est,t-1}+ \frac{\eta||^S_E\hat{q}_{est,t-1}||}{\beta + \eta||^S_E\hat{q}_{est,t-1}||}(\frac{1}{2}^S_E\hat{q}_{est,t-1}\otimes ^Sw_t)\Delta t - \frac{\beta}{\beta + \eta||^S_E\hat{q}_{est,t-1}||}\eta||\frac{1}{2}^S_E\hat{q}_{est,t-1}\otimes ^Sw_t||\Delta t\frac{\bigtriangledown f(^{S}_{E}\hat{q}_{est,t-1}, ^E\hat{y}, ^S\hat{y}_t)}{||\bigtriangledown f(^{S}_{E}\hat{q}_{est,t-1}, ^E\hat{y}, ^S\hat{y}_t)||}$.
2.4 系统流程图
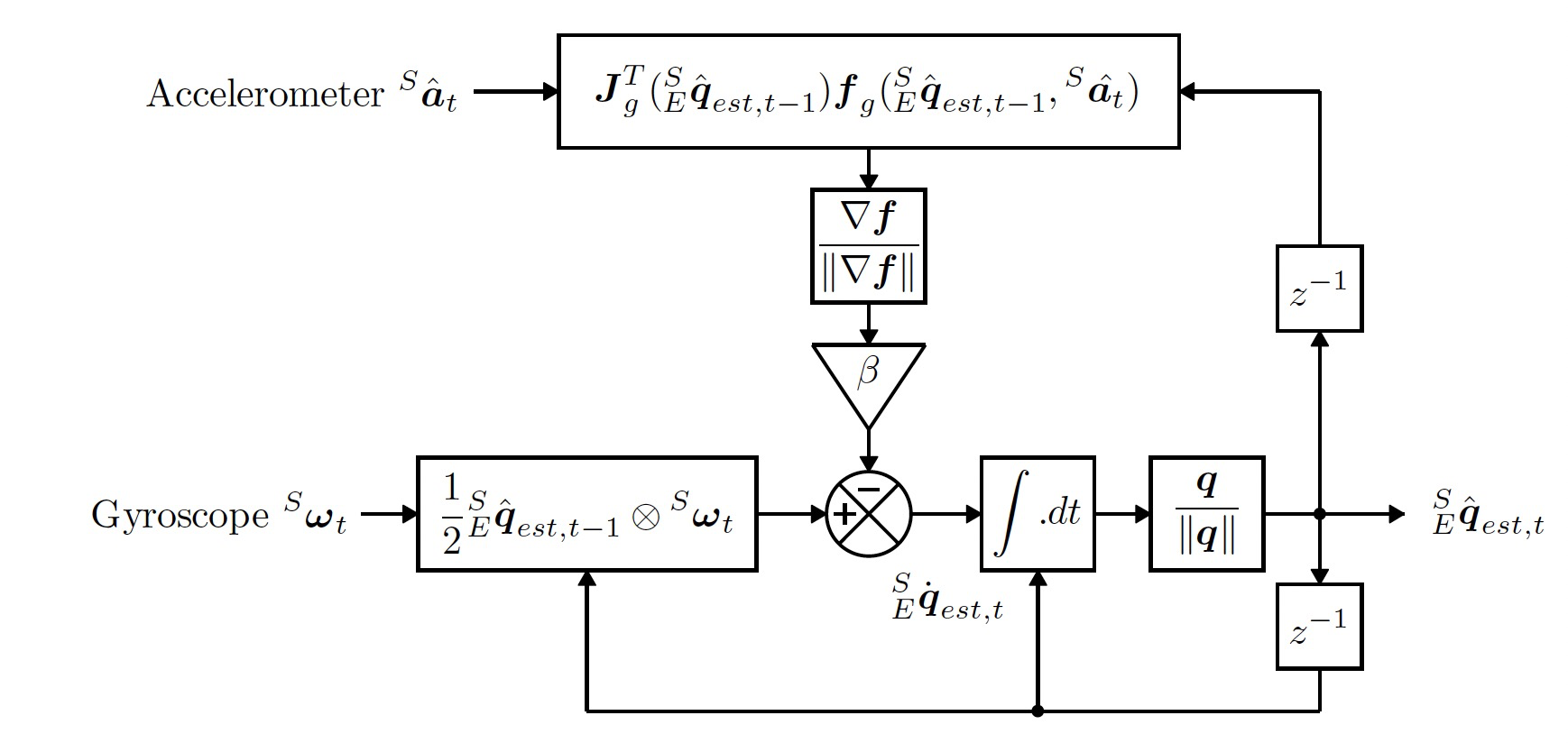
2.5 磁力计校准
- 磁力计易受外界地磁干扰,导致地磁测量数据误差较大
- 磁力计本身也具有误差,例如漂移、制造误差等
如果使用磁力计估计姿态,为了获取精确地姿态,需要对磁力计进行校准
主要思想
- 利用加速度计来校准磁力计
- 因为加速度计不收外界干扰,仅有其自身传感器相关误差
- 采用最优化算法来估计最优姿态,继而校准磁力计
根据论文和参考Madgwick算法详细解读,磁力计校准过程描述如下。
在传感器刚开始运行的时候,即第一帧的时候,传感器可能处于任意一种姿态,几乎不会是水平静止朝北的,所以磁场计的输出$^S\hat{m}_0$几乎不会是$^E\hat{b}_0$。所以,$^E\hat{b}_0$是未知的。此时,可利用加速度计来估计姿态,
$^S\hat{a}_0 = ^S_Eq_0 \otimes ^E\hat{g} \otimes ^S_Eq^*_0$,
用旋转矩阵R表示为,
$^S\hat{a}_0^T = R ^E\hat{g}$.
在上式中,$^S\hat{a}_0$和$^E\hat{g}$是已知的,所以可以由上式再反过来去求出第一帧的姿态$^S_Eq_0$,转换成R,使得f最小,
$\epsilon = R\ ^E\hat{g}^T - ^S\hat{a}^T_0$,
$f = \epsilon^T\epsilon = (R\ ^E\hat{g}^T - ^S\hat{a}_0^T)^T(R\ ^E\hat{g}^T - ^S\hat{a}_0^T)$.
用高斯牛顿迭代法来寻找这个最佳的四元数,其雅克比矩阵为,
$J = [\frac{\partial \epsilon}{\partial q_0}\ \frac{\partial \epsilon}{\partial q_1}\ \frac{\partial \epsilon}{\partial q_2}\ \frac{\partial \epsilon}{\partial q_3}]$.
假设当前四元数各个元素的误差为4行1列的矩阵x,那么$Jx = \epsilon$。采用最小二乘法计算x,
$x = (J^TJ)^{-1}\epsilon$.
所以,现有的四元数的值减去误差,得到新的四元数,
$,^S_E\hat{q}_{0,k+1} = ^S_E\hat{q}_{0,k} - x = ^S_E\hat{q}_{0,k+1} - (J^TJ)^{-1}J^T\epsilon$
其中,$^S_E\hat{q}_{0}$的初始值可以设为$[1\ 0\ 0\ 0]$。
重复上述公式,迭代多次,直到f达到最小值。
于是就得到加速度计估计出的第一帧的姿态$^S_E\hat{q}_{0}$。
根据四元数的坐标系旋转性质,可以把坐标系转到水平的位置上,但并不能保证朝北。对于向量来讲,坐标系逆着四元数转回去,就相当于是向量顺着四元数继续转,得到在这个水平坐标系中的磁场的向量$^E\hat{h}_0$。
其中,$h_x$和$h_y$是$b_x$在这个坐标系中的x轴和y轴上的分量,得到$^E\hat{b}_0 = [0\ \sqrt{h_x^2 + h_y^2}\ 0\ h_z]$.
以上是第一帧的时候得到$^E\hat{b}_0$的方法。
再将加速度计估计出来的姿态$^S_E\hat{q}_{0}$作为初值,将$^E\hat{g}$、$^S\hat{a}_0$、$^E\hat{b}_0$、$^S\hat{m}_0$代入之前公式中,用梯度下降法迭代,得到高精度的第一帧的姿态$^S_E\hat{q}_{0}$。
当物体发生运动之后,由于周围环境的影响,每一帧都要对$^E\hat{b}_t$进行修正,假设上一针的最佳的姿态估计为$^S_R\hat{q}_{est,t-1}$,那么这一帧的$^E\hat{b}_t$为
$^E\hat{h}_t = [0\ h_x\ h_y\ h_z] = ^S_R\hat{q}_{est,t-1} \otimes ^S\hat{m}_t \otimes ^S_R\hat{q}_{est,t-1}^*$,
$^E\hat{b}_t = [0\ \sqrt{h_x^2 + h_y^2}\ 0\ h_z]$.
这样的校准计算可以将外界的电磁干扰影响约束在对传感器指向的方向估计中。而且不需要预先给定地磁方向。
2.6 陀螺仪零点漂移校准
- 陀螺仪的零飘受温度和运动等因素的影响
- 本文提出陀螺仪的零飘可通过姿态变化率来进行弥补
修正方法如下:
$^S_E\dot{\hat{q}}_{\epsilon}$代表了陀螺仪在各个轴的角误差,使用前文提到的$^S_E\dot{q}_{w,t} = \frac{1}{2}^S_E\hat{q}_{est,t-1}\otimes ^Sw_t$公式的逆运算可以得出陀螺仪当前度数的可能偏差为$^Sw_{\epsilon, t} = 2^S_E\hat{q}^*_{est,t-1}\otimes ^S_E\dot{\hat{q}}_{\epsilon,t}$。
那么,陀螺仪随着时间的漂移量为$^Sw_{b,t} = \zeta\sum\ ^Sw_{\epsilon,t}\Delta t$。
最后,得到校正后的陀螺仪读数为$^Sw_{\epsilon,t} = ^Sw_{t} - ^Sw_{b,t}$。
2.7 算法的整体流程
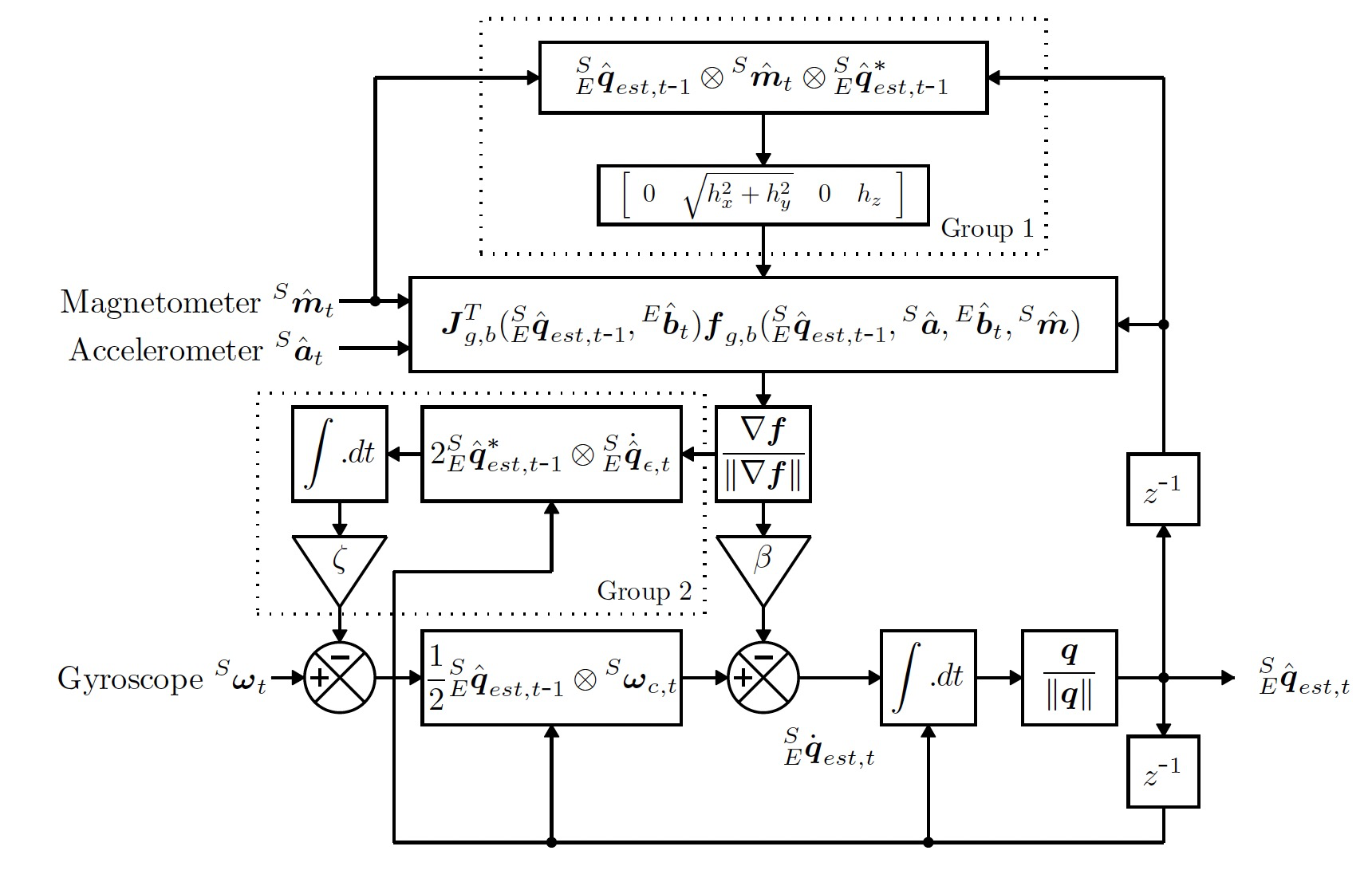
3. 实验评测
3.1 实验设置
- 传感器
- xsens MTx orientation sensor
- tri-axis gyroscopes, accelerometers and magnetometers
- 512 Hz
- 对比算法
- Kalman-based orientation filter
- 真值
- A Vicon system
3.2 实验结果
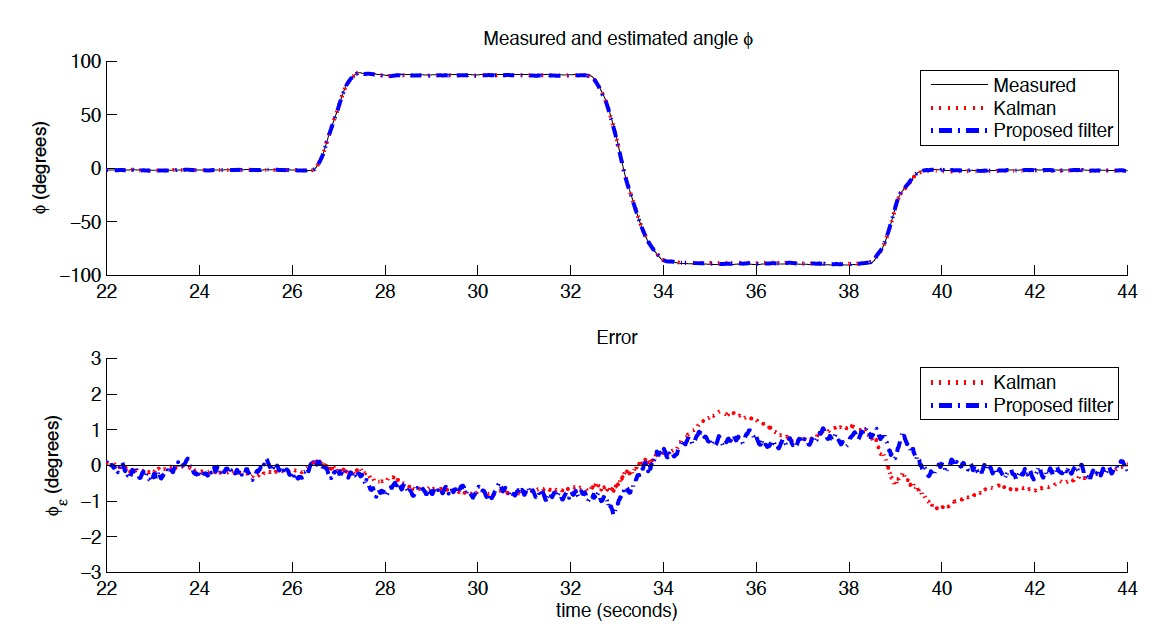
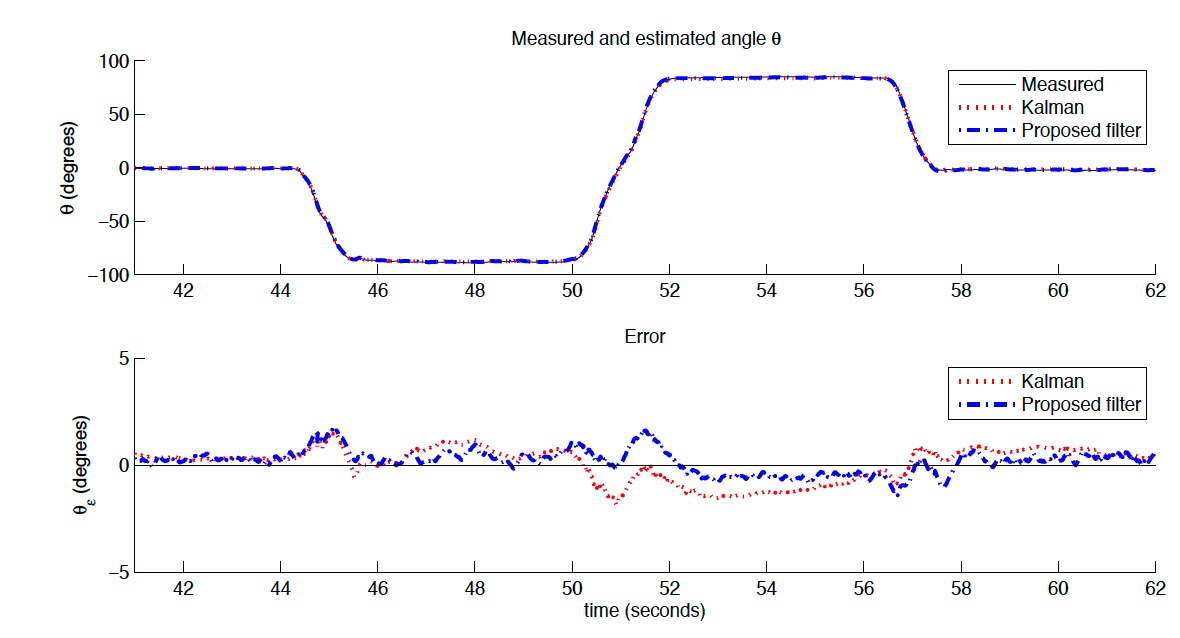
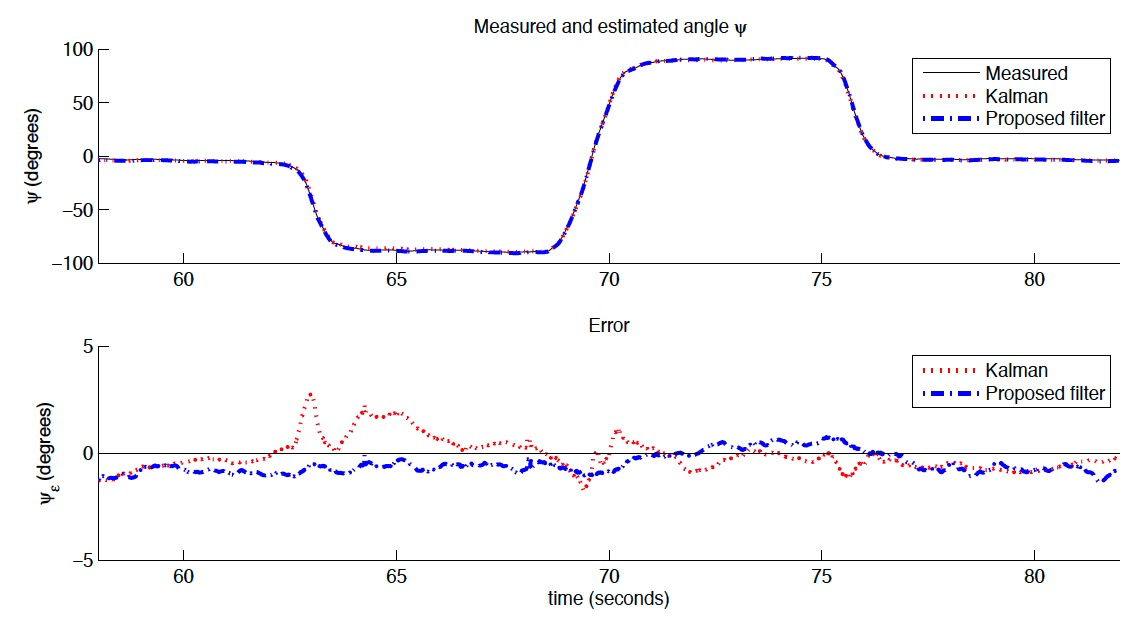
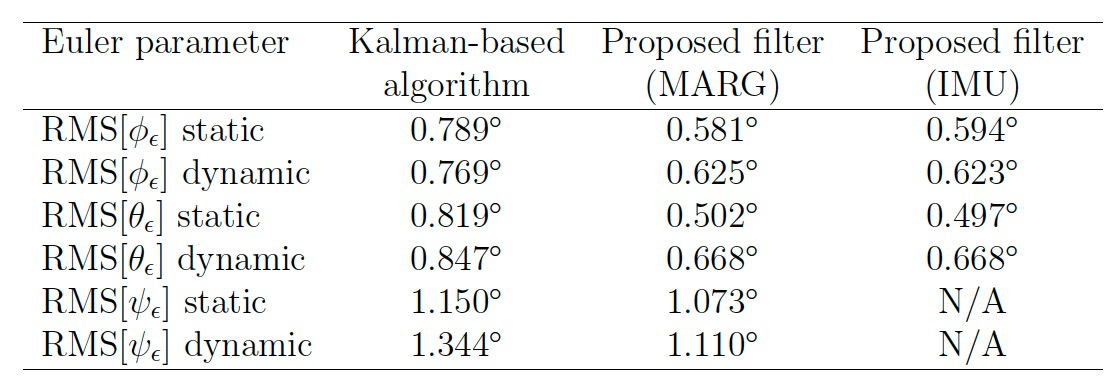
5. 代码实现
5.1 论文源码
- 加速度计和陀螺仪
1 |
|
- 加速度计、陀螺仪和磁力计
1 | // Math library required for `sqrt' |
5.2 x-io源码
- https://x-io.co.uk/open-source-imu-and-ahrs-algorithms/
- MadgwickAHRS.h
1 | //===================================================================================================== |
- MadgwickAHRS.c
1 | //===================================================================================================== |
- MahonyAHRS.h
1 | //===================================================================================================== |
- MahonyAHRS.c
1 | //===================================================================================================== |