数据结构与算法（三）-链表

1. 概述

• 数组需要一块连续的内存空间来存储，对内存的要求比较高，而链表恰恰相反，它并不需要一块连续的内存空间，它通过“指针”将一组零散的内存块串联起来使用
• 内存块称为链表的“结点”
• 为了将所有的结点串起来，每个链表的结点除了存储数据之外，还需要记录链上的下一个结点的地址，把这个记录下个结点地址的指针叫作后继指针 next
• 第一个结点叫作头结点，用来记录链表的基地址，基于头结点，可以遍历得到整条链表
• 最后一个结点叫作尾结点，指向一个空地址 NULL
• 优点
  • 快速插入和删除，时间复杂度为O(1)
• 缺点
  • 无法快速的随机访问第 k 个元素，需要根据指针一个结点一个结点地依次遍历，直到找到相应的结点，时间复杂度为O(n)

2. 单链表

• 结点定义
  • 结点由存放数据元素的数据域存放后继结点地址的指针域组成
  • 假设p是指向线性表第i个元素的指针，则该结点ai的数据域我们可以用p->data来表示，p->data的值是一个数据元素，结点ai的指针域可以用 p->next来表示，p->next的值是一个指针。p->next指向第i+1个元素，即指向ai+1的指针
  • 关于结构体”struct Node *next;”，next是指向下一个Node，所以其类型必须是Node，但是 Node 是结构体，所以前面还得加上个 struct
  • “Node(const int& d): data(d), next(NULL) {}”是结构体的构造函数，d=T()来指定默认值，用构造函数来初始化成员变量data和指针，所有数据类型，默认初始化都为0，这里data默认初始化为0

typedef struct Node {
	ElemType data;
	struct Node *next;
  Node(const ElemType& d = ElemType()): data(d), next(NULL) {}
} Node;
typedef struct Node *LinkList;

如下图所示：

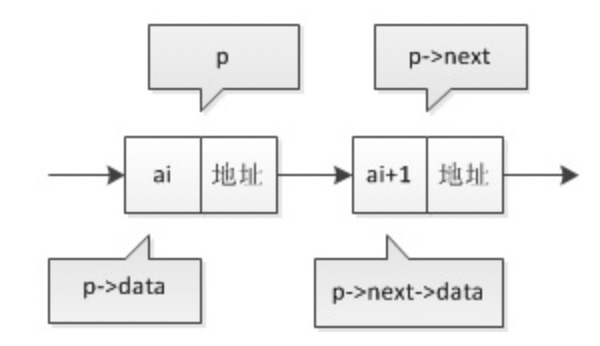
（图片来源：https://blog.csdn.net/sinat_20265495/article/details/52716710）

• 创建头结点
  • 新建节点Node，将Node的next置为NULL

head = new Node(0);
head->next = NULL;

• 从头插入一个新的节点
  • 新建新节点p，p的next的指向head->next所指向的地址
  • head->next指向p

Node * p = new Node(int);
p->next = data->next;
head->next = p;

• 删除指定节点
  • 先遍历到指定节点的前一个节点
  • 将前一个节点的next指针指向指定节点的下一个节点，达到悬空指定节点的效果
  • 删除指定节点

Node * p = find(d);
Node *q = p->next;
p->next = p->next->next;
delete q;

• 修改指定节点
  • 遍历到指定节点的位置
  • 将其data修改为要修改的值

Node *p = find(d);
p->next->data = d_new;

• 链表反转
  • 定义三个临时节点指向头结点之后的第1个节点p，第2个节点q和第3个节点m
  • 将p->next置为空
  • 将q->next = p
  • 将p向后移动一个节点，即p = q
  • 将q向后移动一个节点，即q = m
  • 把m向后移动一个节点，即m = m->next;
  • 依此类推直到m等于NULL
  • 将q->next = p
  • 将head->next指向q（即目前第一个节点，也就是原本最后的一个节点）

Node *p = head->next;
Node *q = head->next->next;
Node *m = head->next->next->next;
p->next = NULL;
while(m) {
    q->next = p;
    p = q;
    q = m;
    m = m->next;
}
q->next = p;
head->next = q;

代码如下:

• List.hpp

//
// Created by Xiaoqiang Teng on 2019/11/30.
//

#ifndef DATA_STRUCTURE_LIST_H
#define DATA_STRUCTURE_LIST_H

#include <iostream>

class List {

public:
    List();
    ~List();

    void CreateList();
    void Insert(const int& d);
    void InsertPos(const int& d, const int& d_new);
    void Erase(const int& d);
    void Updata(const int& d, const int& d_new);
    void Reverse();

    void Print();

private:
    struct Node{
        int data;
        Node * next;
        Node(const int& d):data(d),next(NULL){}
    };

    Node *head;

    void Clear() {
        Node * p = head;
        while(p) {
            Node * q = p->next;
            delete p;
            p = q;
        }
    }

    Node* find(const int& d) {
        Node * p = head;
        for(; p; p = p->next) {
            if(p->next->data == d)
                break;
        }
        return p;
    }

};

#endif //DATA_STRUCTURE_LIST_H

• List.cpp

//
// Created by Xiaoqiang Teng on 2019/11/30.
//

#include "List.h"

List::List() {
    CreateList();
}

List::~List() {
    Clear();
}

void List::CreateList() {
    head = new Node(0);
}

void List::Insert(const int& d) {
    Node *p = new Node(d);
    p->next = head->next;
    head->next = p;
}

void List::InsertPos(const int& d, const int& d_new) {
    Node *p = find(d);
    Node *q = new Node(d_new);
    q->next = p->next;
    p->next = q;

}

void List::Erase(const int& d) {
    Node *p = find(d);
    Node *q = p->next;
    p->next = p->next->next;
    delete q;
}

void List::Updata(const int& d, const int& d_new) {
    Node *p = find(d);
    p->next->data = d_new;
}

void List::Reverse() {
    Node *p = head->next;
    Node *q = head->next->next;
    Node *m = head->next->next->next;
    p->next = NULL;
    while(m) {
        q->next = p;
        p = q;
        q = m;
        m = m->next;
    }
    q->next = p;
    head->next = q;
}

void List::Print() {
    for (Node * p = head->next; p; p = p->next) {
        std::cout << p->data << std::endl;
    }
}

以上代码参考：https://www.cnblogs.com/scandy-yuan/archive/2013/01/06/2847801.html

3. 单向循环链表

• 单向循环链表和单向链表差不多，只不过是最后的尾节点指向的不是空，而是指向头节点
• 优点是从链尾到链头比较方便。当要处理的数据具有环型结构特点时，就特别适合采用循环链表

代码如下：

• CircularList.hpp

//
// Created by Xiaoqiang Teng on 2019/11/30.
//

#ifndef DATA_STRUCTURE_CIRCULARLIST_H
#define DATA_STRUCTURE_CIRCULARLIST_H

#include <iostream>

class Node {
public:
    int data;
    Node *pNext;
};

class CircularList {
public:
    CircularList();
    ~CircularList();

    void CreateList(int n);
    void TraverseLinkList();
    bool IsEmpty();
    int GetLength();
    void InsertNode(int position, int d);
    void DeleteNode(int position);
    void DeleteLinkList();

private:
    Node *head;

};

#endif //DATA_STRUCTURE_CIRCULARLIST_H

• CircularList.cpp

//
// Created by Xiaoqiang Teng on 2019/11/30.
//

#include "CircularList.h"

CircularList::CircularList() {
    head = new Node;
    head->data = 0;
    head->pNext = head;
}

CircularList::~CircularList() {
    delete head;
}

void CircularList::CreateList(int n) {
    if (n < 0) {
        return;
    }
    Node *pnew, *ptemp = head;
    int i = n;
    while (n-- > 0) {
        pnew = new Node;
        pnew->data = n;
        pnew->pNext = head;
        ptemp->pNext = pnew;
        ptemp = pnew;
    }
}

void CircularList::TraverseLinkList() {
    Node *ptemp = head->pNext;
    while (ptemp != head) {
        std::cout << ptemp->data << " ";
        ptemp = ptemp->pNext;
    }
    std::cout << std::endl;
}

bool CircularList::IsEmpty() {
    if (head->pNext == head) {
        return true;
    }
    return false;
}

int CircularList::GetLength() {
    int n = 0;
    Node *ptemp = head->pNext;
    while (ptemp != head) {
        n ++;
        ptemp = ptemp->pNext;
    }
    return n;
}

void CircularList::InsertNode(int position, int d) {
    if (position < 0 || position > GetLength() + 1) {
        return;
    }
    Node *pnew, *ptemp = head;
    pnew = new Node;
    pnew->data = d;
    while (position-- > 1) {
        ptemp = ptemp->pNext;
    }
    pnew->pNext = ptemp->pNext;
    ptemp->pNext = pnew;
}

void CircularList::DeleteNode(int position) {
    if (position < 0 || position > GetLength()) {
        return;
    }
    Node *ptemp = head, *pdelete;
    while (position-- > 1) {
        ptemp = ptemp->pNext;
    }
    pdelete = ptemp->pNext;
    ptemp->pNext = pdelete->pNext;
    delete pdelete;
    pdelete = NULL;
}

void CircularList::DeleteLinkList() {
    Node *pdelete = head->pNext, *ptemp;
    while (pdelete != head) {
        ptemp = pdelete->pNext;
        head->pNext = ptemp;
        delete pdelete;
        pdelete = ptemp;
    }
}

以上代码参考：https://blog.csdn.net/fisherwan/article/details/25561857

4. 双向链表

• 双向链表支持两个方向，每个结点不止有一个后继指针 next 指向后面的结点，还有一个前驱指针 prev 指向前面的结点
• 双向链表需要额外的两个空间来存储后继结点和前驱结点的地址。所以，如果存储同样多的数据，双向链表要比单链表占用更多的内存空间。虽然两个指针比较浪费存储空间，但可以支持双向遍历，这样也带来了双向链表操作的灵活性
• 用空间换时间
• 从结构上来看，双向链表可以支持 O(1) 时间复杂度的情况下找到前驱结点，使双向链表在某些情况下的插入、删除等操作都要比单链表简单、高效
• 优点
  • 插入效率高，双向链表中的结点已经保存了前驱结点的指针，不需要像单链表那样遍历
  • 查找效率高，可以记录上次查找的位置 p，每次查询时，根据要查找的值与 p 的大小关系，决定是往前还是往后查找，所以平均只需要查找一半的数据

参考

• C++ 单链表基本操作分析与实现
• C++版）链表（二）——实现单项循环链表创建、插入、删除等操作