1. 线性方程组
定义:包含未知数的$x_1, x_2, \cdots, x_n$的线性方程组如下所示:
矩阵形式:
系数矩阵为:
增广矩阵为:
1.1 线性方程组的解法
采用等价方程组来求解一个线性方程组。等价方程组可通过如下三种变换得到:
- 把某一个方程换成另一个方程的倍数的和
- 把某一方程的所有项乘以一个非零常数
- 交换两个方程的位置
以上变换即所谓的“行初等变换”。
例:
转换为行阶梯形为:
和最简形为:
相当于:
1.2 存在与唯一性问题
- 线性方程组是否相容
- 若它有解,解的唯一性
2. 行化简与阶梯型矩阵
2.1 阶梯型定义
- 每一非零行在每一零行之上
- 某一行的先导元素所在的列位于前一行先导元素的后面
- 某一行的先导元素所在的列下方元素都是零。
2.2 简化阶梯型
- 属于阶梯型
- 每一非零行的先导元素是1
- 每一先导元素1是该元素所在列的唯一非零元素
2.3 例子
- 行阶梯形
- 行最简形
2.4 主元位置和主元列
距震中的主元位置是矩阵A中对应于它的阶梯形中先导元素的位置;主元列是矩阵A中含有主元位置的列。
2.5 线性方程组的解
应用行化简法解线性方程组:
- 写出方程组的增广矩阵
- 应用行化简算法把增广矩阵化为阶梯形。确定方程组是否有解,如果没有解则停止;否则进行下一步。
- 继续行化简法得到他的简化阶梯形
- 写出由第三步所得矩阵所对应的方程组
- 把第四步所得到的每个方程改写为用自由变量表示基本变量的形式。
3. 向量方程
3.1 $R^{2}$中的向量定义
- 仅含一列的矩阵称为列向量,或简称向量。
- 两个向量相等,当且仅当两个向量对应元素相等。
- 向量是实数的有序对。
- 所有元素都是零的向量称为零向量。
3.2 向量的性质
- 向量u, v, w和标量c和d
- u + v = v + u
- (u + v) + w = u + (v + w)
- u + 0 = 0 + u
- u + (-u) = -u + u = 0
3.3 线性组合
戈丁$R^n$中的向量$v_1, v_2, \dots, v_p$和标量$c_1, c_2, \dots, c_p$,向量$y = c_1v_1 + c_2v_2 + \dots + c_pv_p$称为向量$v_1, v_2, \dots, v_p$以$c_1, c_2, \dots, c_p$为权的线性组合。
定义$Span\{v_1, v_2, \dots, v_n\}$为由$v_1, v_2, \dots, v_n$的所有线性组合所成的集合。
要判断向量b是否属于$Span\{v_1, v_2, \dots, v_n\}$,就是判断向量方程:
是否有解。
3.4 向量方程
向量方程,和增广矩阵为的线性方程组有相同的解集。特别地,b可表示为$a_1, a_2, \dots, a_n$的线性组合,当且仅当上述增广矩阵有解。
线性代数的一个主要思想是研究可以表示为某一固定向量集合$\{v_1, v_2, \dots, v_n\}$的线性组合的所有向量。
4. 矩阵方程
若A是mxn矩阵,它的各列为$a_1, \dots, a_n$。若x是$R^n$中向量,则A与x的积,记为Ax,就是A的各列以x中对应元素为权的线性组合,即:
。
例:
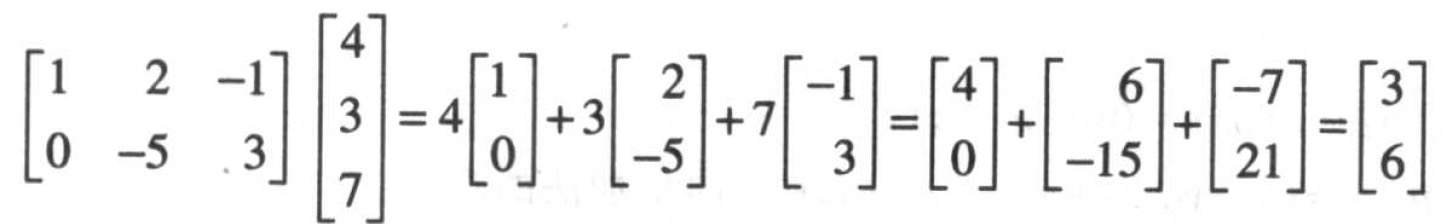
4.1 向量方程和矩阵方程的区别
向量方程形如:
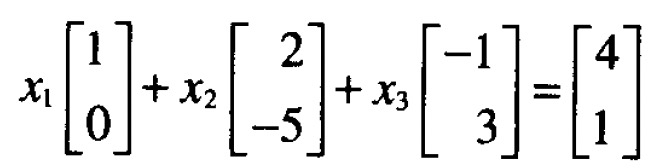
矩阵方程形如:
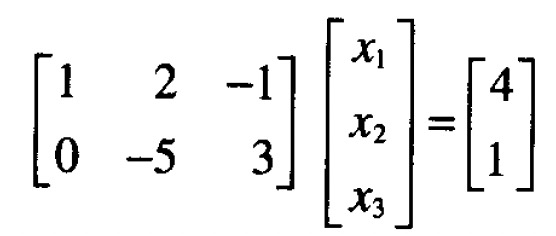
4.2 解的存在性
设A是mxn矩阵,则下列命题是逻辑上等价的。也就是说,对某个A,他们都成立或者都不成立:
- 对$R^{m}$中每个b,方程Ax = b有解
- $R^{m}$中的每个b都是A的列的一个线性组合
- A的各列生成$R^m$
- A的每一行都有一个主元位置
5. 线性方程组的解集
5.1 齐次线性方程组
线性方程组称为齐次的,若它可写成Ax = 0的形式,其中A是mxn矩阵,0是$R^m$中的零向量。这样的方程组至少有一个解,即x = 0。这个解称为它的平凡解。
齐次方程Ax = 0有非平凡解,当且仅当方程至少有一个自由变量。
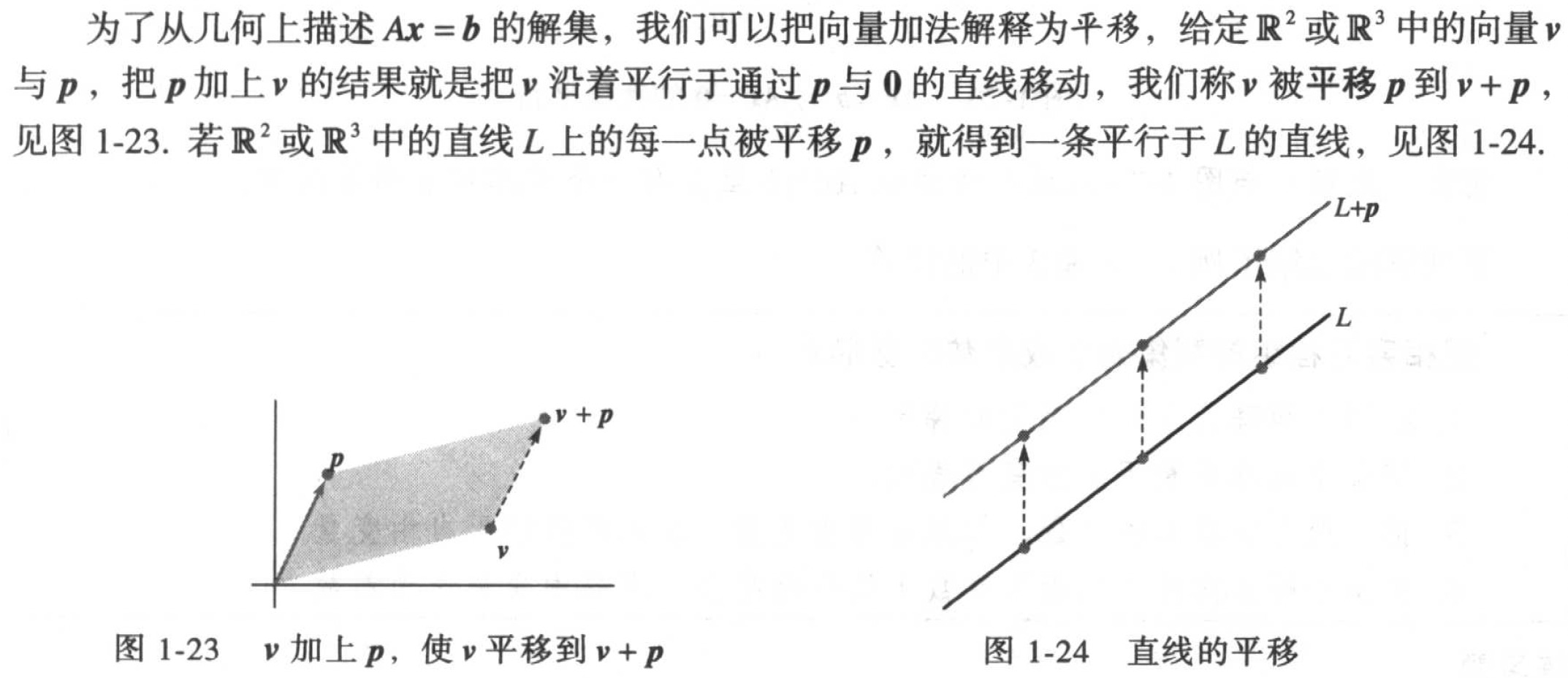
5.2 参数向量形式

方程(2)是称为平面的参数向量方程。有时也可写为:
。
5.3 非齐次方程组的解
当非齐次方程组有许多解时,一般可表示为参数向量形式,即由一个向量加上满足对应的齐次方程的一些向量的任意线性组合的形式。
例:


几何解释:
6. 线性无关
6.1 定义
$R^n$中一组向量$\{v_1, \dots, v_p\}$称为线性无关的,若向量方程$x_1v_1 + x_2v_2 + \dots + x_pv_p = 0$仅有平凡解。向量组(集)称为线性无关的,若存在不全为零的权$c_1, \dots, c_p$,使$c_1v_1 + c_2v_2 + \dots + c_pv_p = 0$。
6.2 矩阵各列的线性无关
矩阵A的各列线性无关,当且仅当方程Ax = 0仅有平凡解。
6.3 一个或多个向量的集合
两个向量的集合$\{v_1, v_2\}$线性相关,当且仅当其中一个向量是另一个向量的倍数。这个集合线性无关,当且仅当其中一个向量都不是另一个向量的倍数。
更多个向量的集合$S = \{v_1, \dots, v_p\}$线性相关,当且仅当S中至少有一个向量是其他向量的线性组合。
若一个向量组的向量个数超过每个向量元素个数,那么这个向量组线性相关。
- 若向量组$S = \{v_1, \dots, v_p\}$包含零向量,则它线性相关。
7. 线性变换介绍
7.1 矩阵变换
变换(或映射)T称为线性的,若:
- 对T的定义域中一切u, v,T(u + v) = T(u) + T(v)
- 对一切u和标量c,T(cu) = cT(u)
7.2 线性变换的矩阵


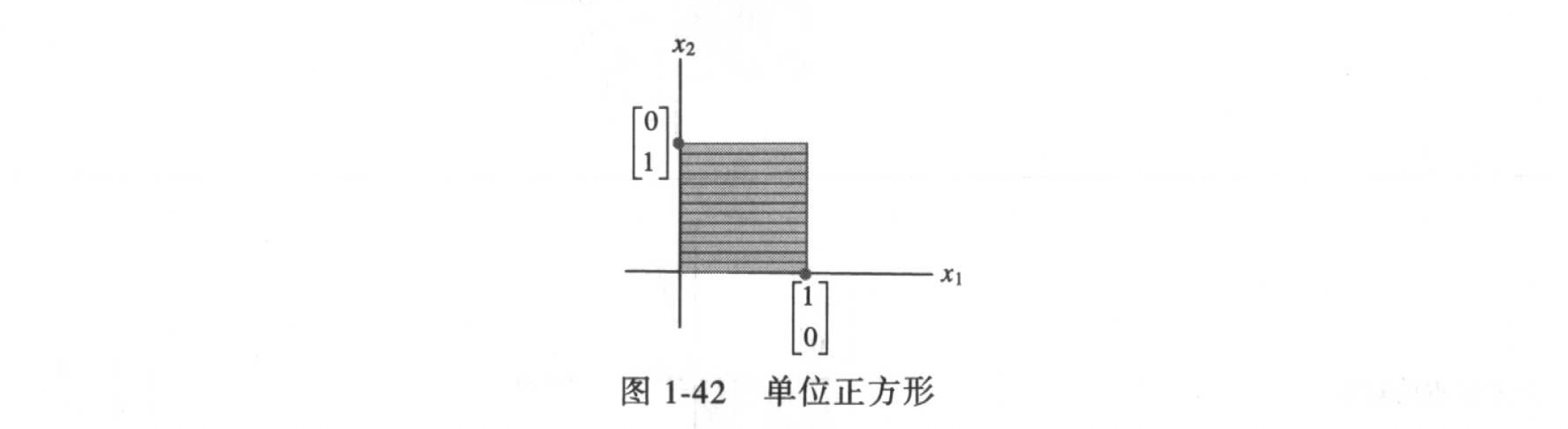
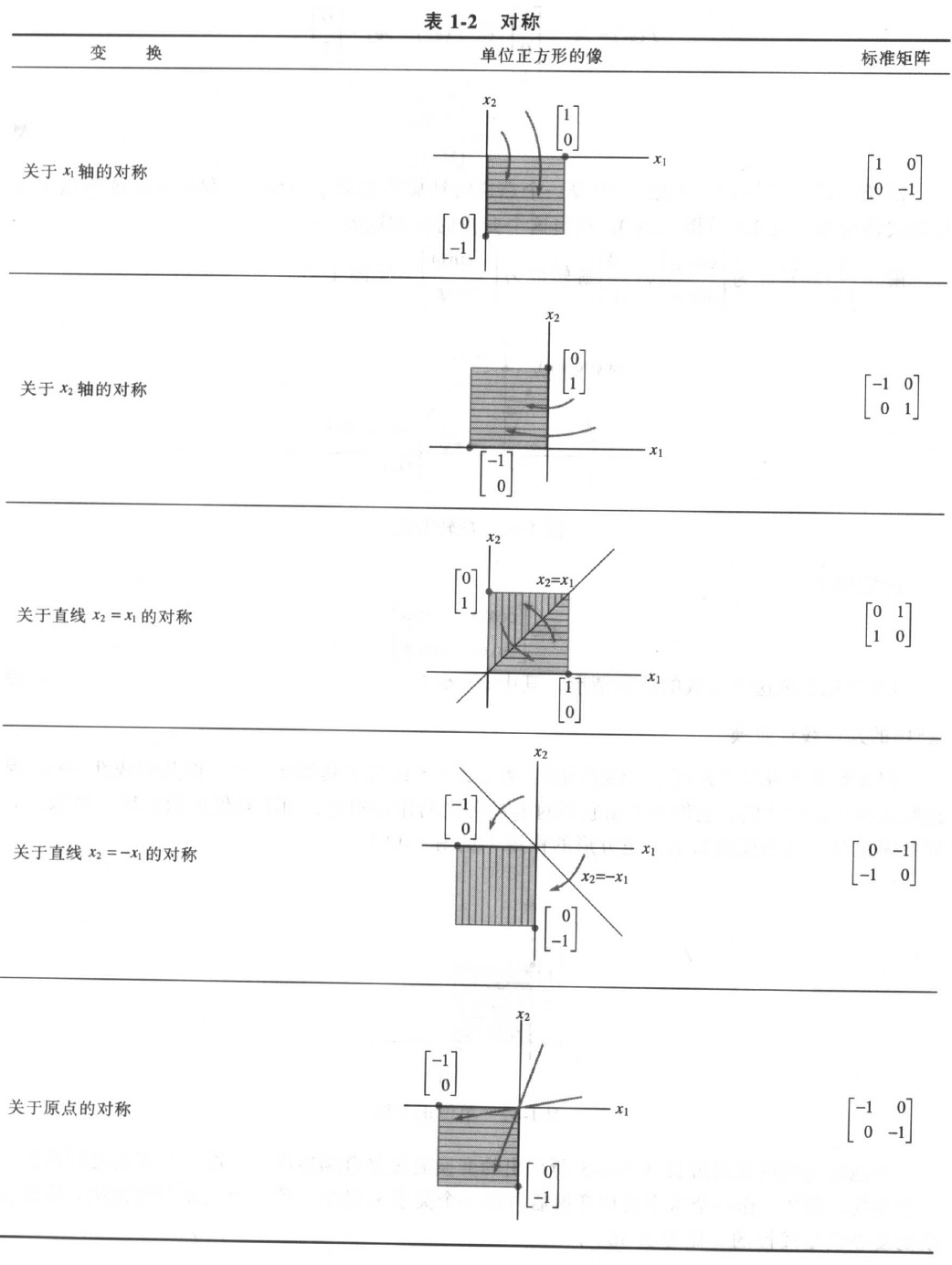
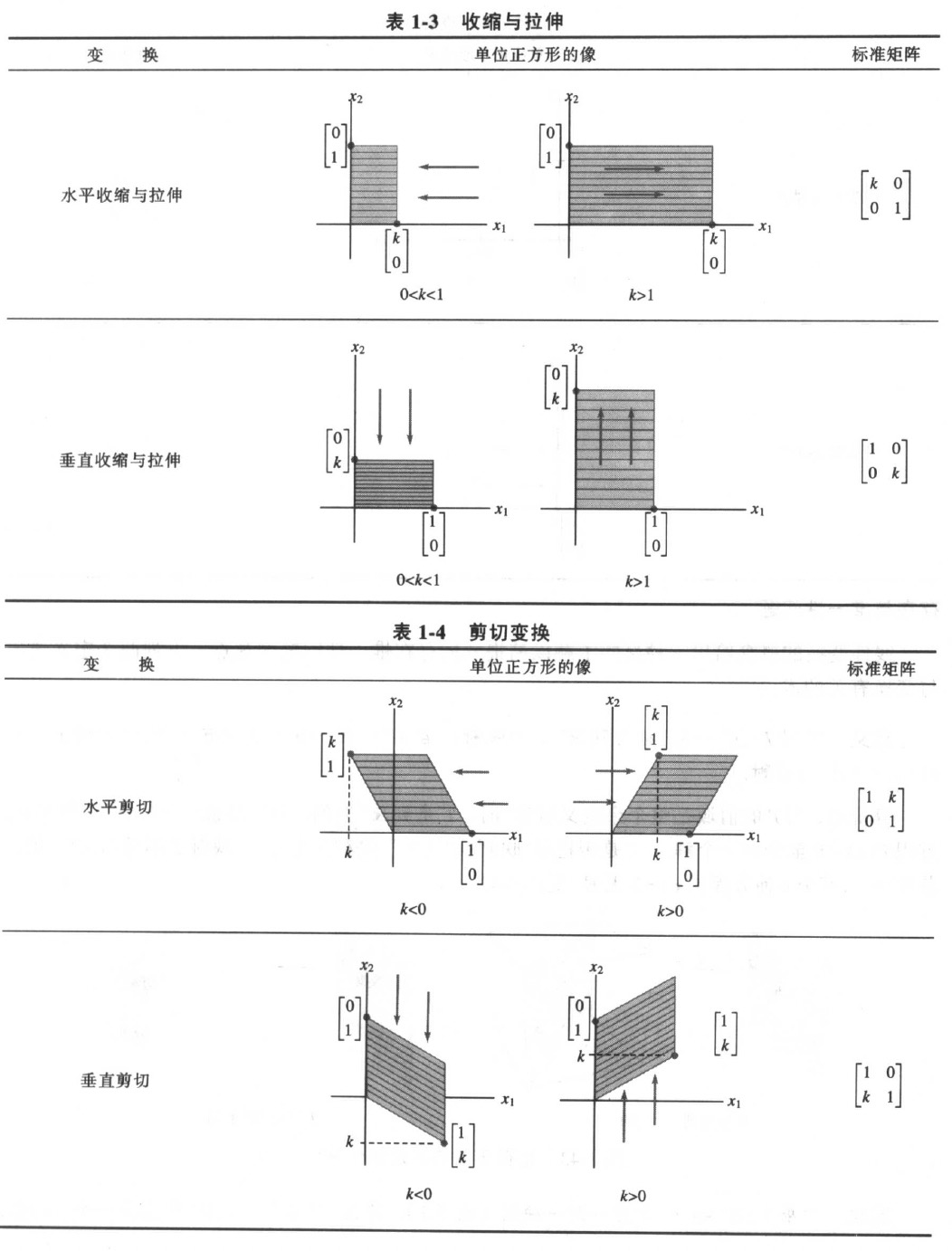
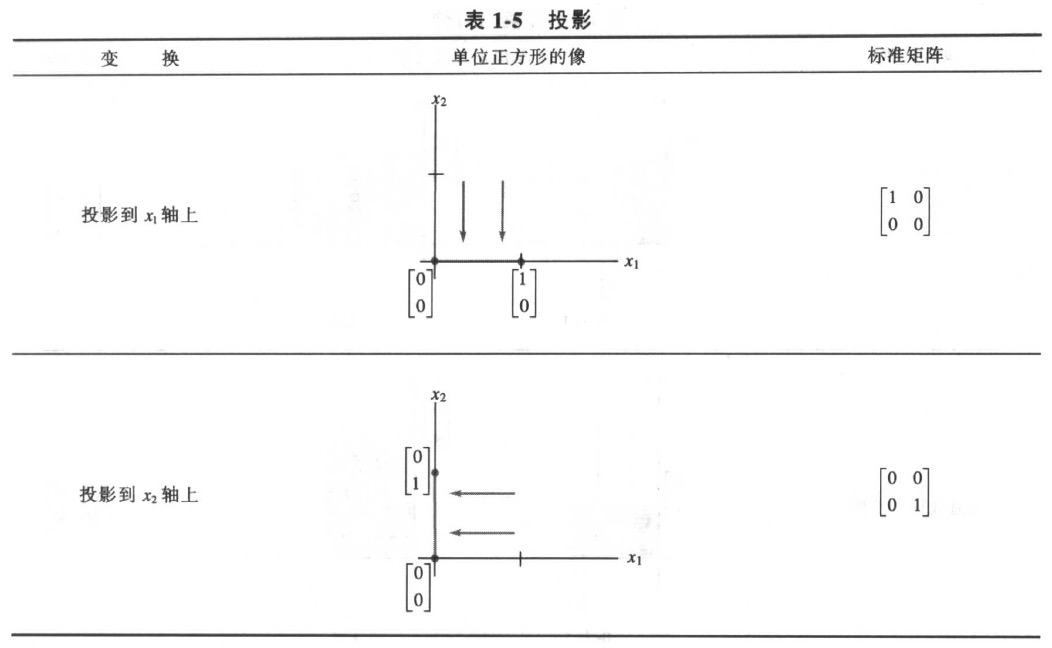
7.3 $R^2$中的几何线性变换
例: